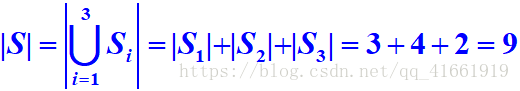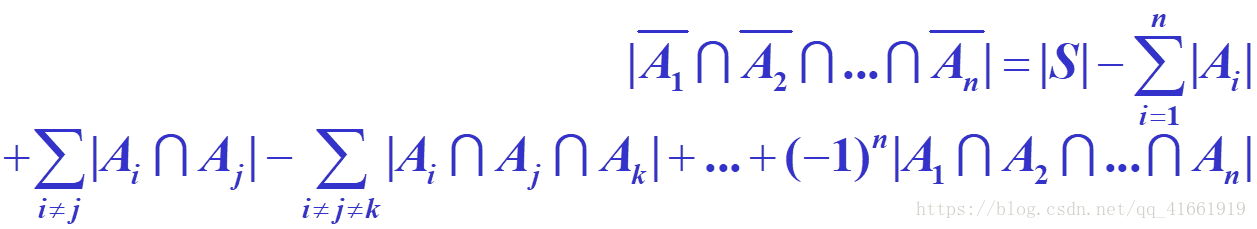組合數學總結

阿新 • • 發佈：2019-02-13

前言：雖然書上的基本知識都看完了，也看懂了，但是對於課本上這一部分的例題，感覺難度還是不小的，可能是自己對於基本知識的理解還不到位，感覺自己可以先做一部分模板題，熟悉一下這些知識，然後再逐漸提升。

一、基礎知識梳理：

1、計數原理：加法原理，乘法原理，鴿巢原理、容斥原理；

①加法原理：即A∪B，（注意A、B之間是互斥的，交集為空集）：

例1、有一所學校給一名物理競賽優勝者發獎，獎品有三類，第一類是三種不同版本的法漢詞典；第二類是四種不同型別的物理參考書；第三類是二種不同的獎盃。這位優勝者只能挑選一樣獎品。那麼，這位優勝者挑選獎品的方法有多少種？

解：設S是所有這些獎品的集合，Si

是第i類獎品的集合(i=1,2,3)，顯然，Si∩Sj=Φ (i≠j) ，根據加法法則有

②乘法原理：即A∩B（A、B之間是相互獨立的)：

例2、從A 地到B地有二條不同的道路，從B地到C地有四條不同的道路，而從C地到D地有三條不同的道路。求從A地經B、C兩地到達D地的道路數。

解：設S是所求的道路數集合，S1、S2、S3分別是從A到B、從B到C、從C到D的道路集合，根據乘法法則有

③鴿巢原理，又稱抽屜原理：

即將n+1個物體放入n個盒子中，則必然至少有一個盒子中放入>=2件的物體。

例3、一個教師每週上7次課，則這教師至少有一天要上至少2次課（星期天不上課除外）。

證明：此例中把“天”當作盒子，

相當於6個盒子放7個物體，從而得證。（注意：鴿籠原理只能說明至少存在這麼一個盒子，但具體是哪一個盒子並不能確定）。

④容斥原理：

首先，我們要知道這麼幾個公式及定理：

1*：DeMorgan定律：設A、B為全集U的兩個子集，則有： $\overline{A\cup B}=\overline{A}\cap \overline{B}$ ，以及 $\overline{A\cap B}= \overline{A}\cup\overline{B}$ ；

定理2： $\left |\overline{A}\cap \overline {B} \right |=\left |S \right |-\left |A \right |-\left |B \right |+\left |A\cap B \right |$

由上述兩式可以推廣到n件事件的情況。

3*容斥定理：

$若Ai (i=1,2,…,n) S，且Ai是S中具有性質pi的元素的子集，則S中不具有性質pi (i=1,2,…,n)的元素的個數為：$ Ai (i=1,2,…,n) ∈S，且Ai是S中具有性質pi的元素的子集，則S中不具有性質pi (i=1,2,…,n)的元素的個數為：

2、婚姻配對問題（G-S演算法）：

其原理大概是：男的依次向自己喜歡的女生表白，如果女生還沒有男友或者該男生比女生的現男友優秀，則表白成功，反之，表白失敗，在下一輪中再向其它女生表白，如此迴圈，直至所有男生與女生配對。難點在於資訊的記錄與儲存上。

其次對於該問題主要就是模板的應用了。。。POJ3487\HDU1522。

3、組合問題分類：存在、計數、構造、最優。（找規律\遞推）

4、排列：

①：n個元素中可重複的選出m個元素的排列，排列方案數： $n^{m}$ 。

②：n個元素中有 $n_{1}$ 個相同元素， $n_{2}$ 個相同元素...... $n_{m}$ 個相同元素，且 $n_{1}+n_{2}+......+n_{m}=n$ ，則n個元素中取r各元素的選排列方案總數為 $\frac{A_{n} ^{r}}{n_{1}!*n_{2}!*...*n_{m}!}$ 。