動態規劃 ------最大子段和
1.最大子段和的問題描述

2.動態規劃的求解:

3.優化函數的遞推方程

4.動態規劃求解偽碼

5.動態規劃求解的小結:

動態規劃的代碼:
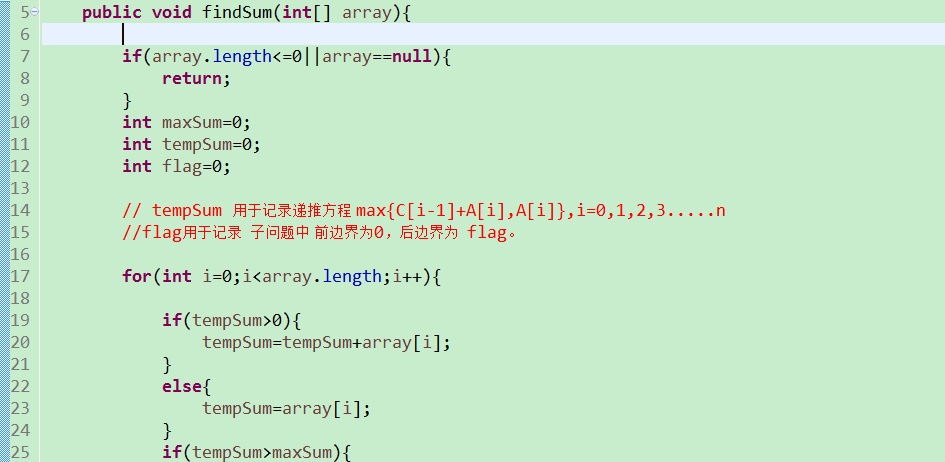
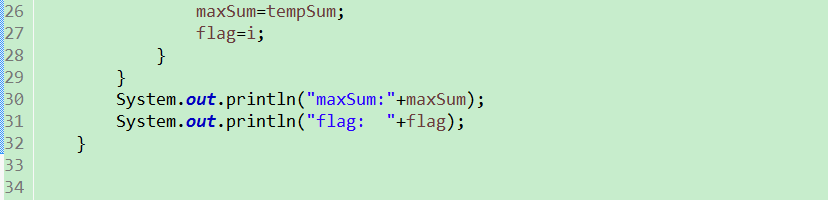
動態規劃 ------最大子段和
相關推薦
動態規劃 ------最大子段和
動態規劃 函數 cnblogs png 規劃 font 3-9 .cn -- 1.最大子段和的問題描述 2.動態規劃的求解: 3.優化函數的遞推方程 4.動態規劃求解偽碼 5.動態規劃求解的小結: 動態規劃的
POJ-1050 動態規劃最大子段和最大子陣
1、最大子段 由於最大子段不可能以負數或負數段開頭,可以以此得到演算法 int max(int a[],int n) { int sum,maxsum; int i ; sum = maxsum = 0; for(i =
動態規劃 最大子段和
mes 最小 最大的 iostream ace 動態規劃 strong 最大值 ffffff 子段與子段和的概念: 給定一個由數字組成的序列,其中一段連續的序列稱為一個子段(假設非空),子段中所有的數字和就是為 子段和 例子: {1,2,3,4} ,
LeetCode-初級=動態規劃-最大子序和
給定一個整數陣列 nums ,找到一個具有最大和的連續子陣列(子陣列最少包含一個元素),返回其最大和。 示例: 輸入: [-2,1,-3,4,-1,2,1,-5,4], 輸出: 6 解釋: 連續子陣列 [4,-1,2,1] 的和最大,為 6。 進階: 如果你已經實現
poj1050(動態規劃+最大子矩陣和)
題目要求是輸入一個N*N的矩陣,然後求出這個矩陣的最大子矩陣和,在一維空間中是求最大連續字串和,這題也算是它在二維空間裡的一個擴充套件吧…… 這個動歸先求第i行第j列在這一行從1到j的最大字串和,然後
分治法/動態規劃-最大子序和
給定一個整數陣列 nums ,找到一個具有最大和的連續子陣列(子陣列最少包含一個元素),返回其最大和。 示例: 輸入: [-2,1,-3,4,-1,2,1,-5,4], 輸出: 6 解釋: 連續子陣列 [4,-1,2,1] 的和最大,為 6。 分治
[C++] 動態規劃之矩陣連乘、最長公共子序列、最大子段和、最長單調遞增子序列
每次 種子 () return 避免 amp 可能 text com 一、動態規劃的基本思想 動態規劃算法通常用於求解具有某種最優性質的問題。在這類問題中,可能會有許多可行解。每一個解都對應於一個值,我們希望找到具有最優值的解。 將待求解問題分解成若幹個子問題,先求
51Nod1050 迴圈陣列最大子段和(動態規劃)
這題區間是可以迴圈的,如果不迴圈的狀態轉移方程是 if(dp[i-1]>0) dp[i]=dp[i-1]+a[i]; else dp[i]=a[i]; 現在題目要求是可以迴圈,分為兩種情況: 1、沒有迴圈,找到了最大的子段。 2、迴圈了,找到了最大的子段。 第一
最大子段和與最長遞增子序列(貪心與動態規劃)
話不多說先上程式碼。。。。。 最大子段和 題目描述 給出一段序列,選出其中連續且非空的一段使得這段和最大。 輸入輸出格式 輸入格式: 第一行是一個正整數NNN,表示了序列的長度。 第二行包含NNN個絕對值不大於100001000010000的
[洛谷]P1115 最大子段和 (#動態規劃 -1.6)
題目描述 給出一段序列,選出其中連續且非空的一段使得這段和最大。 輸入輸出格式 輸入格式: 第一行是一個正整數NN,表示了序列的長度。 第二行包含NN個絕對值不大於10000的整數Ai,描述
演算法優化:最大子段和,最大子矩陣和,一維,二維情況分析,動態規劃
最大子段和,前面b[j]理解的是:終點在j的最大連續子段和,及從k:j最大和 是對b[j]進行動態規劃,從k:j最大和:取決於k:j-1的最大和,他大於0的話,就為k:j-1的最大和+arr[j],他小於0的話,就只是arr[j] 終點在j一共有n種情況,原問題只是求b[
poj 1050 To the Max(動態規劃處理二維最大子段和)
2、題目大意: 給一個N,然後給定一個N*N的二維陣列,然後求一個子矩陣,使得其中的數加起來和最大 3、思路: 將二維陣列轉換成一維陣列,假設二維陣列是M行N列,那麼將二維陣列分成N條,用dp[i]記錄第i列的和(可以是任意連續長度,for迴圈就能實現),那麼將dp[i]
最大子段和問題:蠻力、遞迴及動態規劃
問題描述 求一個序列的最大子段和即最大連續子序列之和。例如序列[4, -3, 5, -2, -1, 2, 6, -2]的最大子段和為11=[4+(-3)+5+(-2)+(-1)+(2)+(6)]。 1. 蠻力演算法 思想:從序列首元素開始窮舉
動態規劃;最大子段和;溫故而知新-。-;這個動規公式找的很聰明;
1. #include <iostream> 2. using namespace std; 3. 4. class MaxSum 5. { 6. private: 7. int maxS
3981 動態最大子段和
void sam tdi mat 兩個 for inline -h push 題目描述 Description 題目還是簡單一點好... 有n個數,a[1]到a[n]。 接下來q次查詢,每次動態指定兩個數l,r,求a[l]到a[r]的最大子段和。 子段的意思是連續非空
codevs 3981 動態最大子段和(線段樹)
輸入 typedef fault namespace 一行 scrip img sum spl 題目傳送門:codevs 3981 動態最大子段和 題目描述 Description 題目還是簡單一點好... 有n個數,a[1]到a[n]。 接下來q次查詢,每次動
動態最大子段和
build res \n names d+ using 最大子段和 mes its #include <bits/stdc++.h> using namespace std; const int maxn=5e5+10; inline int read(){
演算法設計與分析--求最大子段和問題(蠻力法、分治法、動態規劃法) C++實現
演算法設計與分析--求最大子段和問題 問題描述: 給定由n個整陣列成的序列(a1,a2, …,an),求該序列形如 的子段和的最大值,當所有整數均為負整數時,其最大子段和為0。 利用蠻力法求解: int maxSum(int a[],int n) { int ma
最大子段和問題-蠻力法、分治法、動態規劃法
蠻力法:int maxSum1(int a[], int n){ int i; int j; int maxSum = 0; for(i = 0; i < n; i++){ int sum = 0; fo
hdu 1024 Max Sum Plus Plus(動態規劃+m子段和的最大值)
Now I think you have got an AC in Ignatius.L's "Max Sum" problem. To be a brave ACMer, we always challenge ourselves to more difficult problems. Now you ar
