[POJ2409]Let it Bead - Polya定理
阿新 • • 發佈:2017-12-02
height man 括號 other 簡單的 gcd bre 得到 values [POJ2409]Let it Bead
A bracelet is a ring-like sequence of s beads each of which can have one of c distinct colors. The ring is closed, i.e. has no beginning or end, and has no direction. Assume an unlimited supply of beads of each color. For different values of s and c, calculate the number of different bracelets that can be made. 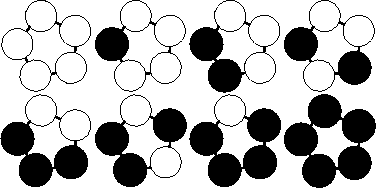 For each test case output on a single line the number of unique bracelets. The figure below shows the 8 different bracelets that can be made with 2 colors and 5 beads.
For each test case output on a single line the number of unique bracelets. The figure below shows the 8 different bracelets that can be made with 2 colors and 5 beads.
| Time Limit: 1000MS | Memory Limit: 65536K |
Description
"Let it Bead" company is located upstairs at 700 Cannery Row in Monterey, CA. As you can deduce from the company name, their business is beads. Their PR department found out that customers are interested in buying colored bracelets. However, over 90 percent of the target audience insists that the bracelets be unique. (Just imagine what happened if two women showed up at the same party wearing identical bracelets!) It‘s a good thing that bracelets can have different lengths and need not be made of beads of one color. Help the boss estimating maximum profit by calculating how many different bracelets can be produced.A bracelet is a ring-like sequence of s beads each of which can have one of c distinct colors. The ring is closed, i.e. has no beginning or end, and has no direction. Assume an unlimited supply of beads of each color. For different values of s and c, calculate the number of different bracelets that can be made.
Input
Output
 For each test case output on a single line the number of unique bracelets. The figure below shows the 8 different bracelets that can be made with 2 colors and 5 beads.
For each test case output on a single line the number of unique bracelets. The figure below shows the 8 different bracelets that can be made with 2 colors and 5 beads.
Sample Input
1 1 2 1 2 2 5 1 2 5 2 6 6 2 0 0
Sample Output
1 2 3 5 8 13 21
題目大意
給出一串長為s的環,用c種顏色染色,可以翻轉可以旋轉,問有多少種不同的,即兩兩之間不能通過翻轉或旋轉得到的染色方法?
題解
看到這種題目,便想到了Polya定理(What‘s that?)。
如果不知什麽是置換以及Polya定理,請戳上面的鏈接。
先考慮旋轉的置換:
共n個置換
對於翻轉m次(翻轉一次就是翻360°/n,或第k+m個元素變為第k個元素的值),一共有gcd(n,m)個循環節(1≤m≤n)
我們記S1=∑sgcd(n,m) (1≤m≤n)
接著考慮翻轉的置換:
能發現一共也是n個置換
其次可以發現,偶數和奇數翻轉的情況不一樣
那麽我們分類討論
首先討論最簡單的奇數:
那當然是從每個點對半切開
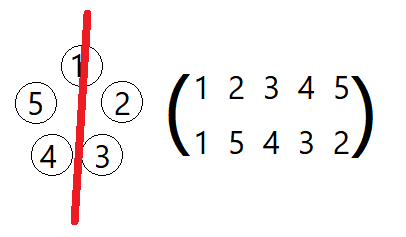
然後可以容易地發現對於每個點都有(n+1)/2個置換
那麽我們記S2=n*s(n+1)/2
然後是偶數的情況
類似於奇數
但是有兩種情況
1:從相對的兩點切開,共n/2個置換,每個有(n+2)/2個循環節
2:切開後兩邊都是n/2個點,共n/2個置換,每個有n/2個循環節
那麽我們記S2=n/2*s(n+2)/2 + n/2*sn/2=(s+1)*n/2*sn/2
根據公式
可以算出最終的答案
其中|G|=2n,右邊括號裏邊的和即之前的S1+S2
Ans=(S1+S2)/2n
代碼如下:
1 #include <iostream> 2 #include <cstdio> 3 using namespace std; 4 #define LLI long long 5 int gcd(int a,int b){ 6 return b==0?a:gcd(b,a%b); 7 } 8 int fastpow(int a,int b){int res=1; 9 for(;b;b>>=1,a=a*a)if(b&1)res=a*res;return res;} 10 int main(){ 11 int a,b;LLI ans; 12 while(scanf("%d%d",&a,&b)==2){ 13 if(a==0&&b==0)break; 14 ans=0; 15 for(int i=1;i<=b;++i)ans+=fastpow(a,gcd(i,b)); 16 if(b&1)ans+=1LL*b*fastpow(a,b+1>>1); 17 else ans+=1LL*(a+1)*(b>>1)*fastpow(a,b>>1); 18 ans/=b<<1; 19 printf("%lld\n",ans); 20 } 21 return 0; 22 }
代碼寫的有點醜……
[POJ2409]Let it Bead - Polya定理
