生日悖論
阿新 • • 發佈:2018-11-09
計算生日悖論概率
假設一個班級有n個人,那麼計算這n個人至少有兩個人生日相同的概率。 一般情況下,我們感性認識上會覺得班級上至少有兩個人生日相同的概率會比較低,畢竟每個人的生日有365種選擇,而班級一半隻有30人左右,但是實際上計算得到的至少兩人生日相同的概率卻遠遠大於我們的感性認識,所以稱為生日悖論。
計算生日概率:
假設班級有n個人,我們從反面計算至少有兩個人生日相同的概率,這個反面就是每個人生日都不同的概率。那麼這個概率可以這麼計算:
- 第一個同學的生日有365種選擇;
- 第二的同學的生日有364種選擇,這裡是因為要保證每個人的生日都不同,所以已經選擇過的日期不能再選。
- 第三個同學的生日有363種選擇;
- 第四個同學的生日有362種選擇;
- 第i個同學的生日有365 - i + 1種選擇;
這n位同學的總的選擇的數量為:
所以,假設班級上 n 位同學的生日都不相同的概率為:
然後,包含 n 位同學的一個班級,至少有兩位同學生日相同的概率為:
替換公式中的生日不同的概率公式
所以 n 位同學中至少有兩位生日相同的概率:
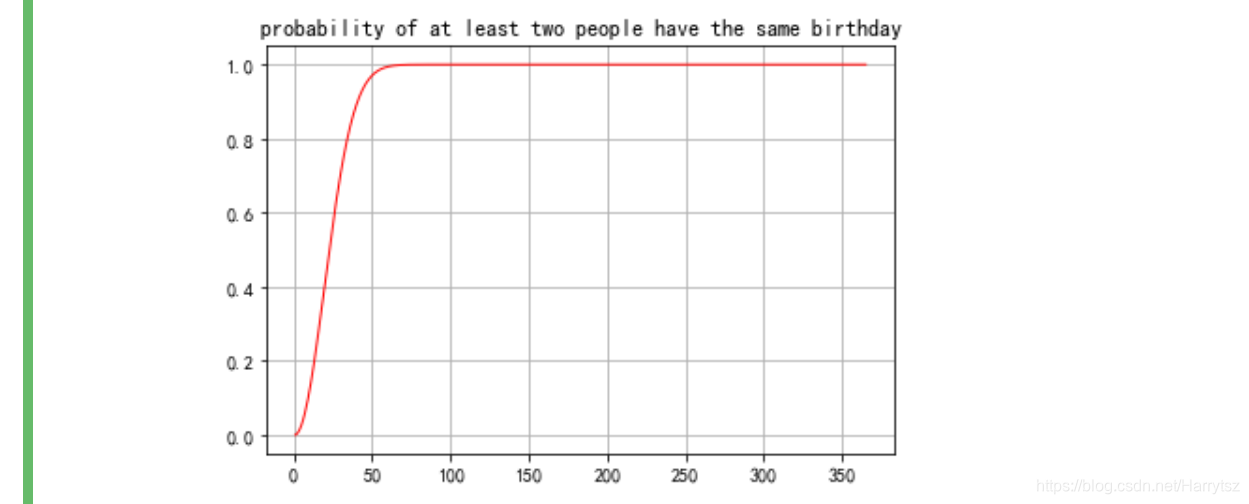
| n | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
|---|---|---|---|---|---|---|---|---|---|
| P | 0.12 | 0.25 | 0.41 | 0.57 | 0.71 | 0.81 | 0.89 | 0.94 | 0.97 |
程式碼如下:
import math
class Solution(object):
def computeProb(self, n):
"""
:type n: int
:rtype: float
Idea: if n > 365, then definitely at least two people will has the same birthday,
when n <= 365, we compute the probability of that these people do not have same birthday,
1th people have 365 choice, 2nd people has 364 choice, 3rd people has 363 choice, etc.
Using log operation to avoid float multipy overflow
"""
assert n > 0, 'n should > 0'
if n > 365:
return 1.0
prob = 0.0
for i in range(n):
prob += math.log((365 - i) / 365.0, 2)
return 1.0 - 2.0 ** prob
class BirthdayParadoxImage(object):
def showCurve(self):
x = [i + 1 for i in range(365)]
y = []
prob = 0.0
for n in x:
prob += math.log((365 - n + 1) / 365.0, 2)
current_prob = 1.0 - 2.0 ** prob
y.append(current_prob)
import matplotlib.pyplot as plt
plt.title('probability of at least two people have the same birthday')
plt.plot(x, y, color='red', lw=1)
plt.grid(b=True)
plt.show()
if __name__ == '__main__':
so = Solution()
print(str(so.computeProb(10)) + ', probability of 10 people')
print(str(so.computeProb(15)) + ', probability of 15 people')
print(str(so.computeProb(20)) + ', probability of 20 people')
print(str(so.computeProb(25)) + ', probability of 25 people')
print(str(so.computeProb(30)) + ', probability of 30 people')
print(str(so.computeProb(35)) + ', probability of 35 people')
print(str(so.computeProb(40)) + ', probability of 40 people')
print(str(so.computeProb(45)) + ', probability of 45 people')
print(str(so.computeProb(50)) + ', probability of 50 people')
print('show curve')
image = BirthdayParadoxImage()
image.showCurve()