1. 正則化的目的：防止過擬合！

2. 正則化的本質：約束（限制）要優化的引數。

關於第1點，過擬合指的是給定一堆資料，這堆資料帶有噪聲，利用模型去擬合這堆資料，可能會把噪聲資料也給擬合了，這點很致命，一方面會造成模型比較複雜（想想看，本來一次函式能夠擬合的資料，現在由於資料帶有噪聲，導致要用五次函式來擬合，多複雜！），另一方面，模型的泛化效能太差了（本來是一次函式生成的資料，結果由於噪聲的干擾，得到的模型是五次的），遇到了新的資料讓你測試，你所得到的過擬合的模型，正確率是很差的。

關於第2點，本來解空間是全部區域，但通過正則化添加了一些約束，使得解空間變小了，甚至在個別正則化方式下，解變得稀疏了。這一點不得不提到一個圖，相信我們都經常看到這個圖，但貌似還沒有一個特別清晰的解釋，這裡我嘗試解釋一下，圖如下：

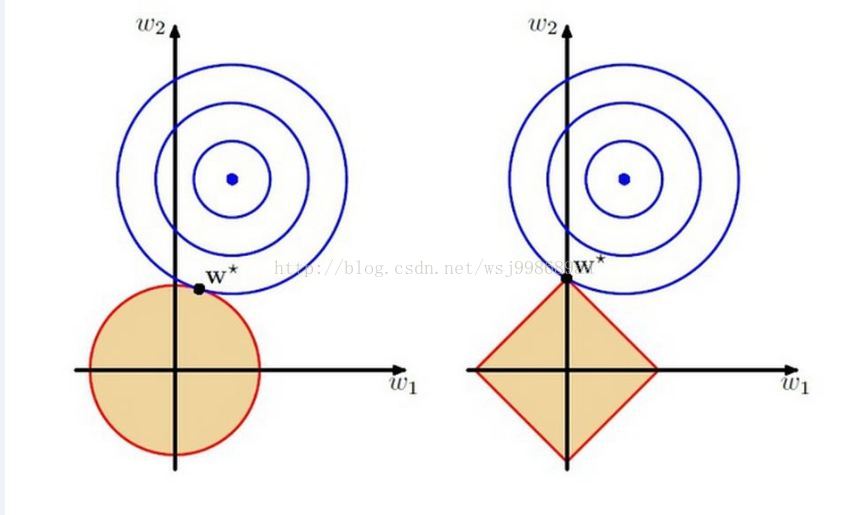
這裡的w1，w2都是模型的引數，要優化的目標引數，那個紅色邊框包含的區域，其實就是解空間，正如上面所說，這個時候，解空間“縮小了”，你只能在這個縮小了的空間中，尋找使得目標函式最小的w1，w2。左邊圖的解空間是圓的，是由於採用了L2範數正則化項的緣故，右邊的是個四邊形，是由於採用了L1範數作為正則化項的緣故，大家可以在紙上畫畫，L2構成的區域一定是個圓，L1構成的區域一定是個四邊形。

再看看那藍色的圓圈，再次提醒大家，這個座標軸和特徵（資料）沒關係，它完全是引數的座標系，每一個圓圈上，可以取無數個w1，w2，這些w1，w2有個共同的特點，用它們計算的目標函式值是相等的！那個藍色的圓心，就是實際最優引數，但是由於我們對解空間做了限制，所以最優解只能在“縮小的”解空間中產生。

藍色的圈圈一圈又一圈，代表著引數w1，w2在不停的變化，並且是在解空間中進行變化（這點注意，圖上面沒有畫出來，估計畫出來就不好看了），直到脫離了解空間，也就得到了圖上面的那個w*，這便是目標函式的最優引數。

對比一下左右兩幅圖的w*，我們明顯可以發現，右圖的w*的w1分量是0，有沒有感受到一絲絲涼意？稀疏解誕生了！是的，這就是我們想要的稀疏解，我們想要的簡單模型。

還記得模式識別中的剃刀原理不？傾向於簡單的模型來處理問題，避免採用複雜的。

這裡必須要強調的是，這兩幅圖只是一個例子而已，沒有說採用L1範數就一定能夠得到稀疏解，完全有可能藍色的圈圈和四邊形（右圖）的一邊相交，得到的就不是稀疏解了，這要看藍色圈圈的圓心在哪裡。

此外，正則化其實和“帶約束的目標函式”是等價的，二者可以互相轉換。關於這一點，我試著給出公式進行解釋：

針對上圖（左圖），可以建立數學模型如下：

通過熟悉的拉格朗日乘子法（注意這個方法的名字），可以變為如下形式：

看到沒，這兩個等價公式說明了，正則化的本質就是，給優化引數一定約束，所以，正則化與加限制約束，只是變換了一個樣子而已。

此外，我們注意，正則化因子，也就是裡面的那個lamda，如果它變大了，說明目標函式的作用變小了，正則化項的作用變大了，對引數的限制能力加強了，這會使得引數的變化不那麼劇烈（僅對如上數學模型），直接的好處就是避免模型過擬合。反之，自己想想看吧。。。

個人感覺，“正則化”這幾個字叫的實在是太抽象了，會嚇唬到人，其實真沒啥。如果改成“限制化”或者是“約束化”.