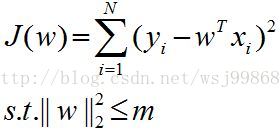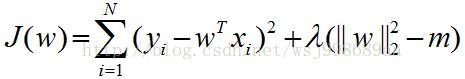談談自己對正則化的一些理解~
上學的時候,就一直很好奇,模式識別理論中,常提到的正則化到底是幹什麼的?漸漸地,聽到的多了,看到的多了,再加上平時做東西都會或多或少的接觸,有了一些新的理解。
1. 正則化的目的:防止過擬合!
2. 正則化的本質:約束(限制)要優化的引數。
關於第1點,過擬合指的是給定一堆資料,這堆資料帶有噪聲,利用模型去擬合這堆資料,可能會把噪聲資料也給擬合了,這點很致命,一方面會造成模型比較複雜(想想看,本來一次函式能夠擬合的資料,現在由於資料帶有噪聲,導致要用五次函式來擬合,多複雜!),另一方面,模型的泛化效能太差了(本來是一次函式生成的資料,結果由於噪聲的干擾,得到的模型是五次的),遇到了新的資料讓你測試,你所得到的過擬合的模型,正確率是很差的。
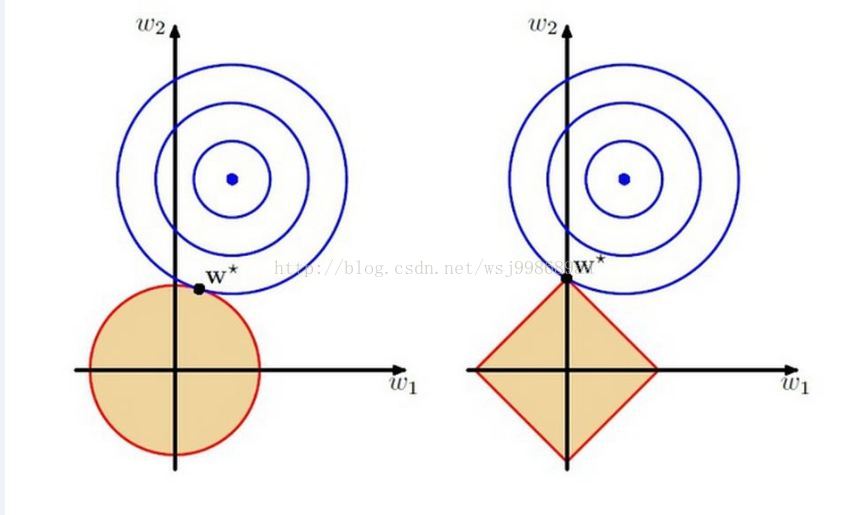
關於第2點,本來解空間是全部區域,但通過正則化添加了一些約束,使得解空間變小了,甚至在個別正則化方式下,解變得稀疏了。這一點不得不提到一個圖,相信我們都經常看到這個圖,但貌似還沒有一個特別清晰的解釋,這裡我嘗試解釋一下,圖如下:
這裡的w1,w2都是模型的引數,要優化的目標引數,那個紅色邊框包含的區域,其實就是解空間,正如上面所說,這個時候,解空間“縮小了”,你只能在這個縮小了的空間中,尋找使得目標函式最小的w1,w2。左邊圖的解空間是圓的,是由於採用了L2範數正則化項的緣故,右邊的是個四邊形,是由於採用了L1範數作為正則化項的緣故,大家可以在紙上畫畫,L2構成的區域一定是個圓,L1構成的區域一定是個四邊形。
再看看那藍色的圓圈,再次提醒大家,這個座標軸和特徵(資料)沒關係,它完全是引數的座標系,每一個圓圈上,可以取無數個w1,w2,這些w1,w2有個共同的特點,用它們計算的目標函式值是相等的!那個藍色的圓心,就是實際最優引數,但是由於我們對解空間做了限制,所以最優解只能在“縮小的”解空間中產生。
藍色的圈圈一圈又一圈,代表著引數w1,w2在不停的變化,並且是在解空間中進行變化(這點注意,圖上面沒有畫出來,估計畫出來就不好看了),直到脫離了解空間,也就得到了圖上面的那個w*,這便是目標函式的最優引數。
對比一下左右兩幅圖的w*,我們明顯可以發現,右圖的w*的w1分量是0,有沒有感受到一絲絲涼意?稀疏解誕生了!是的,這就是我們想要的稀疏解,我們想要的簡單模型。
還記得模式識別中的剃刀原理不?傾向於簡單的模型來處理問題,避免採用複雜的。
這裡必須要強調的是,這兩幅圖只是一個例子而已,沒有說採用L1範數就一定能夠得到稀疏解,完全有可能藍色的圈圈和四邊形(右圖)的一邊相交,得到的就不是稀疏解了,這要看藍色圈圈的圓心在哪裡。
此外,正則化其實和“帶約束的目標函式”是等價的,二者可以互相轉換。關於這一點,我試著給出公式進行解釋:
針對上圖(左圖),可以建立數學模型如下:
通過熟悉的拉格朗日乘子法(注意這個方法的名字),可以變為如下形式:
看到沒,這兩個等價公式說明了,正則化的本質就是,給優化引數一定約束,所以,正則化與加限制約束,只是變換了一個樣子而已。
此外,我們注意,正則化因子,也就是裡面的那個lamda,如果它變大了,說明目標函式的作用變小了,正則化項的作用變大了,對引數的限制能力加強了,這會使得引數的變化不那麼劇烈(僅對如上數學模型),直接的好處就是避免模型過擬合。反之,自己想想看吧。。。
個人感覺,“正則化”這幾個字叫的實在是太抽象了,會嚇唬到人,其實真沒啥。如果改成“限制化”或者是“約束化”,豈不是更好?
相關推薦
談談自己對正則化的一些理解~
上學的時候,就一直很好奇,模式識別理論中,常提到的正則化到底是幹什麼的?漸漸地,聽到的多了,看到的多了,再加上平時做東西都會或多或少的接觸,有了一些新的理解。 1. 正則化的目的:防止過擬合! 2. 正則化的本質:約束(限制)要優化的引數。 關於第1點,過擬合指的是給定一
對L1正則化和L2正則化的理解
一、 奧卡姆剃刀(Occam's razor)原理: 在所有可能選擇的模型中,我們應選擇能夠很好的解釋資料,並且十分簡單的模型。從貝葉斯的角度來看,正則項對應於模型的先驗概率。可以假設複雜模型有較小的先驗概率,簡單模型有較大的先驗概率。 二、正則化項
L1和L2正則化直觀理解
正則化是用於解決模型過擬合的問題。它可以看做是損失函式的懲罰項,即是對模型的引數進行一定的限制。 應用背景: 當模型過於複雜,樣本數不夠多時,模型會對訓練集造成過擬合,模型的泛化能力很差,在測試集上的精度遠低於訓練集。 這時常用正則化來解決過擬合的問題,常用的正則化有L1正則化和L2
L1正則化與L2正則化的理解
一、概括: L1和L2是正則化項,又叫做罰項,是為了限制模型的引數,防止模型過擬合而加在損失函式後面的一項。 二、區別: 1.L1是模型各個引數的絕對值之和。 L2是模型各個引數的平方和的開方值。 2.L1會趨向於產生少量的特徵,而其他的特徵都是0. 因為最優的引數值很大概率
dropout和L1,L2正則化的理解筆記
理解dropout from http://blog.csdn.net/stdcoutzyx/article/details/49022443 123 開篇明義,dropout是指在深度學習網路的訓練過程中,對於神經網路單元,按照一定的概率將其暫時從網路
談談我對SOFA模組化的理解
今天我們談談SOFA模組化,首先看一段SOFA的介紹: SOFABoot是螞蟻金服開源的基於Spring Boot的研發框架,它在Spring Boot的基礎上,提供了諸如 Readiness Check,類隔離,日誌空間隔離等能力。在增強了Spring Boot的同時,SOFABoot提供了讓使用者可以在
Batch 、weight decay、momentum、normalization和正則化的一些理解和借鑑
整理一下之前看過的內容,方便後面忘記時查詢。 談談深度學習中的 Batch_Size Batch_Size(批尺寸)是機器學習中一個重要引數,涉及諸多矛盾,下面逐一展開。 首先,為什麼需要有 Batch_Size 這個引數? Batch 的選擇,首先決定的是下降的方向。
關於機器學習當中的正則化、範數的一些理解
The blog is fantastic! What I want to know is why we should regularlize and how we can regularlize, fortunately, this article tells all
自己對類與物件一些粗略的理解
突然有那麼一會會不想動專案,拿出java核心技術再次翻閱,到了物件與類一張,突然跟著概念仔細考慮了一下他們之間的淵源和關係,產生了一點點具象化的理解。 根據面對物件設計的思想,我們可以知道一個物件是類的一個例項。 怎麼理解呢?就好比,水果是一個大類,
簡單理解正則化。
1. 正則化的目的:防止過擬合! 2. 正則化的本質:約束(限制)要優化的引數。 關於第1點,過擬合指的是給定一堆資料,這堆資料帶有噪聲,利用模型去擬合這堆資料,可能會把噪聲資料也給擬合了,這點很致命,一方面會造成模型比較複雜(想想看,本來一次函式能夠擬合的資料,現在由於資料帶有噪聲,導致要
三個層面、三個不同角度理解正則化
全文摘要 “正則化”這是機器學習和深度學習都在不斷用到的一個技術手段,也是解決模型模型過擬合最常用的手段,但是很少有文章真正講的深入徹底,本文是在之前自己的一篇博文的基礎之上進行補充的,將再次從“三個不同層面”解釋正則化,本文只針對L1、L2正則化。 三個不同層面理解“正則化
[work*] 機器學習中正則化項L1和L2的直觀理解
正則化(Regularization) 機器學習中幾乎都可以看到損失函式後面會新增一個額外項,常用的額外項一般有兩種,一般英文稱作-norm和-norm,中文稱作L1正則化和L2正則化,或者L1範數和L2範數。 L1正則化和L2正則化可以看做是損失函式的懲罰項。所謂『懲罰
[一種通用的正則化方法Dropout] 深入理解Dropout正則化思想和實現方法
論文題目: Dropout: A Simple Way to Prevent Neural Networks from Overfitting (1)過擬合問題: 具有大量引數的深度神經網路是非常強大的機器學習系統。然而,在這樣的網路中,過度擬合是一個嚴重的問題。 包含多個非線性隱含
機器學習中正則化項L1和L2的直觀理解
正則化(Regularization) 機器學習中幾乎都可以看到損失函式後面會新增一個額外項,常用的額外項一般有兩種,一般英文稱作ℓ1ℓ1-norm和ℓ2ℓ2-norm,中文稱作L1正則化和L2正則化,或者L1範數和L2範數。 L1正則化和L2正則化可以看做
【機器學習】從貝葉斯角度理解正則化緩解過擬合
從貝葉斯角度理解正則化緩解過擬合 原始的Linear Regression 假設有若干資料 (x1,y1),(x2,y2),...,(xm,ym),我們要對其進行線性迴歸。也就是得到一個方程 y=ωTx+ϵ 注意,這裡忽略偏置,或者可以認為偏
正則化對深層神經網路的影響分析
本文是基於吳恩達老師《深度學習》第二週第一課練習題所做,目的在於探究引數初始化對模型精度的影響。一、資料處理本文所用第三方庫如下,其中reg_utils 和 testCases_regularization為輔助程式從這裡下載。import numpy as np impor
談談自己對教育的理解(K12)
博主是剛剛從985高校本科畢業的應屆生,作為一個已經經歷過小學到高中教育,在大學期間也做過多次家教,小學,初中,高中的學生都有帶過的畢業生,我想還是可以談談自己對教育(k12)的
簡單談談自己對SSH框架的理解
J2EE開發框架其實也是jar類庫,大部分是對原生方法的封裝。目的是為了簡化開發人員的工作,規範開發過程。學習框架即學習其核心原理和配置。 但java世界的框架五花八門,但萬變不離其宗,只有真正掌握了SSH框架的核心機制和設計理念才能輕鬆的學好其他框架。 下面談談我對SSH
正則化的簡單理解
正則性(regularity),正則性衡量了函式光滑的程度,正則性越高,函式越光滑。(光滑衡量了函式的可導性,如果一個函式是光滑函式,則該函式無窮可導,即任意n階可導)。由高等數學知識得知,任何一個函式f(X)都可以通過多項式的模擬得到,即f(X)=θ0+θ1X1+···
[深度學習]更好地理解正則化:視覺化模型權重分佈
在機器學習中,經常需要對模型進行正則化,以降低模型對資料的過擬合程度,那麼究竟如何理解正則化的影響?本文嘗試從視覺化的角度來解釋其影響。 首先,正則化通常分為三種,都是在loss函式的基礎上外加一項: L0: ,即不等於0的元素個數 L1: ,即所有元素的絕對值之和