CS229 6.3 Neurons Networks Gradient Checking

阿新 • • 發佈：2018-11-27

BP演算法很難除錯，一般情況下會隱隱存在一些小問題，比如（off-by-one error），即只有部分層的權重得到訓練，或者忘記計算bais unit，這雖然會得到一個正確的結果，但效果差於準確BP得到的結果。

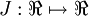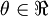有了cost function，目標是求出一組引數W，b，這裡以 $\textstyle \theta$ 表示，cost function 暫且記做 $\textstyle J(\theta)$ 。假設 $\textstyle J : \Re \mapsto \Re$ ，則 $\textstyle \theta \in \Re$ ，即一維情況下的Gradient Descent:

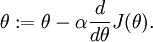
$\begin{align} \theta := \theta - \alpha \frac{d}{d\theta}J(\theta). \end{align}$

根據6.2中對單個引數單個樣本的求導公式：

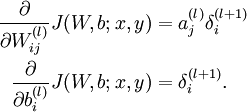
$\begin{align} \frac{\partial}{\partial W_{ij}^{(l)}} J(W,b; x, y) &= a^{(l)}_j \delta_i^{(l+1)} \\ \frac{\partial}{\partial b_{i}^{(l)}} J(W,b; x, y) &= \delta_i^{(l+1)}. \end{align}$

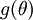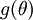可以得到每個引數的偏導數，對所有樣本累計求和，可以得到所有訓練資料對引數 $\textstyle \theta$ 的偏導數記做 $\textstyle g(\theta)$ ， $\textstyle g(\theta)$ 是靠BP演算法求得的，為了驗證其正確性，看下圖回憶導數公式：

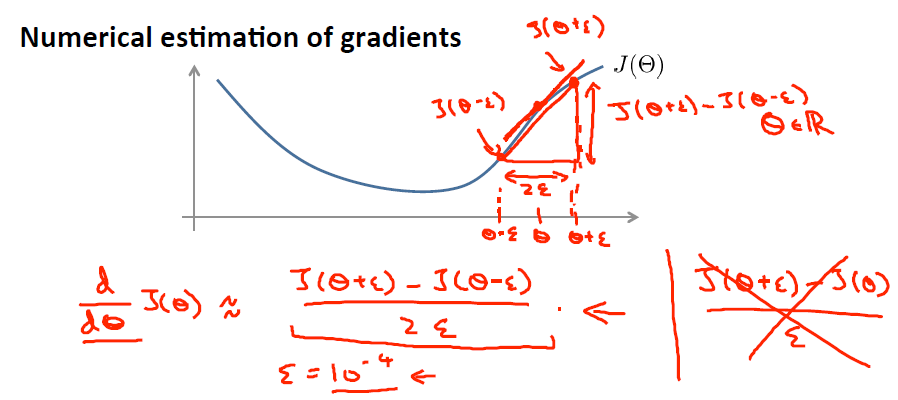
可見有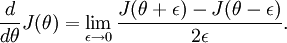： $\begin{align} \frac{d}{d\theta}J(\theta) = \lim_{\epsilon \rightarrow 0} \frac{J(\theta+ \epsilon) - J(\theta-\epsilon)}{2 \epsilon}. \end{align}$ 那麼對於任意 $\textstyle \theta$ 值，我們都可以對等式左邊的導數用：

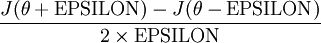$\begin{align} \frac{J(\theta+{\rm EPSILON}) - J(\theta-{\rm EPSILON})}{2 \times {\rm EPSILON}} \end{align}$ 來近似。

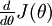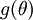給定一個被認為能計算 $\textstyle \frac{d}{d\theta}J(\theta)$ 的函式 $\textstyle g(\theta)$ ，可以用下面的數值檢驗公式

$\begin{align} g(\theta) \approx \frac{J(\theta+{\rm EPSILON}) - J(\theta-{\rm EPSILON})}{2 \times {\rm EPSILON}}. \end{align}$

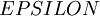應用時，通常把 $\textstyle EPSILON$ 設定為一個很小的常量，比如在 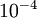$\textstyle 10^{-4}$ 數量級，最好不要太小了，會造成數值的舍入誤差。上式兩端值的接近程度取決於 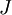$\textstyle J$ 的具體形式。假定 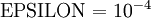$\textstyle {\rm EPSILON} = 10^{-4}$ 的情況下，上式左右兩端至少有4位有效數字是一樣的（通常會更多）。

當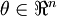 $\textstyle \theta \in \Re^n$ 是一個n維向量而不是實數時，且 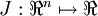$\textstyle J: \Re^n \mapsto \Re$ ，在 Neorons Network 中，J（W，b）可以想象為 W，b 組合擴充套件而成的一個長向量 $\textstyle \theta$

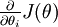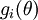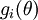，現在又一個計算 $\textstyle \frac{\partial}{\partial \theta_i} J(\theta)$ 的函式 $\textstyle g_i(\theta)$ ，如何檢驗 $\textstyle g_i(\theta)$ 能否輸出到正確結果呢，用 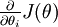$\textstyle \frac{\partial}{\partial \theta_i} J(\theta)$ 的取值來檢驗，對於向量的偏導數：

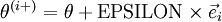根據上圖，對 $\textstyle \theta$ _i求導時，只需要在向量的第i維上進行加減操作，然後求值即可，定義 $\textstyle \theta^{(i+)} = \theta + {\rm EPSILON} \times \vec{e}_i$ ，其中

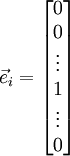
$\begin{align} \vec{e}_i = \begin{bmatrix}0 \\ 0 \\ \vdots \\ 1 \\ \vdots \\ 0\end{bmatrix} \end{align}$

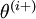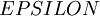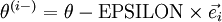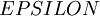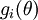$\textstyle \theta^{(i+)}$ 和 $\textstyle \theta$ 幾乎相同，除了第 $\textstyle i$ 行元素增加了 $\textstyle EPSILON$ ，類似地， $\textstyle \theta^{(i-)} = \theta - {\rm EPSILON} \times \vec{e}_i$ 得到的第 $\textstyle i$ 行減小了 $\textstyle EPSILON$ ，然後求導並與 $\textstyle g_i(\theta)$ 比較：

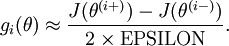
$\begin{align} g_i(\theta) \approx \frac{J(\theta^{(i+)}) - J(\theta^{(i-)})}{2 \times {\rm EPSILON}}. \end{align}$

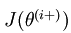中的引數對應的是引數向量中一個分量的細微變化，損失函式J 在不同情況下會有不同的值（比如三層NN 或者三層autoencoder（需加上稀疏項）），上式中左邊為BP演算法的結果，右邊為真正的梯度，只要兩者很接近，說明BP演算法是在正確工作，對於梯度下降中的引數是按照如下方式進行更新的：

$\begin{align} W^{(l)} &= W^{(l)} - \alpha \left[ \left(\frac{1}{m} \Delta W^{(l)} \right) + \lambda W^{(l)}\right] \\ b^{(l)} &= b^{(l)} - \alpha \left[\frac{1}{m} \Delta b^{(l)}\right] \end{align}$

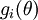即有 $\textstyle g_i(\theta)$ 分別為：

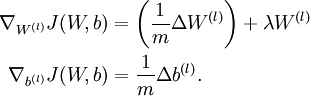
$\begin{align} \nabla_{W^{(l)}} J(W,b) &= \left( \frac{1}{m} \Delta W^{(l)} \right) + \lambda W^{(l)} \\ \nabla_{b^{(l)}} J(W,b) &= \frac{1}{m} \Delta b^{(l)}. \end{align}$

最後只需總體損失函式J(W，b)的偏導數與上述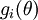 $\textstyle g_i(\theta)$ 的值比較即可。

除了梯度下降外，其他的常見的優化演算法：1) 自適應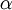 $\textstyle \alpha$ 的步長，2) BFGS L-BFGS，3) SGD，4) 共軛梯度演算法，以後涉及到再看。

CS229 6.3 Neurons Networks Gradient Checking

CS229 6.3 Neurons Networks Gradient Checking

CS229 6.4 Neurons Networks Autoencoders and Sparsity

CS229 6.2 Neurons Networks Backpropagation Algorithm

CS229 6.5 Neurons Networks Implements of Sparse Autoencoder

CS229 6.7 Neurons Networks whitening

CS229 6.9 Neurons Networks softmax regression

CS229 6.8 Neurons Networks implements of PCA ZCA and whitening

CS229 6.10 Neurons Networks implements of softmax regression

CS229 6.12 Neurons Networks from self-taught learning to deep network

CS229 6.11 Neurons Networks implements of self-taught learning

CS229 6.14 Neurons Networks Restricted Boltzmann Machines

CS229 6.13 Neurons Networks Implements of stack autoencoder

CS229 6.15 Neurons Networks Deep Belief Networks

CS229 6.17 Neurons Networks convolutional neural network（cnn）

CS229 6.16 Neurons Networks linear decoders and its implements

(六) 6.1 Neurons Networks Representation

Improving Deep Neural Networks Gradient Checking Homework

CS229 6.6 Neurons Networks PCA主成分分析

macOS10.12部署sonarqube5.6.3 + mysql5.7.17

Jira 6.3.6（破解）+SVN+apache

CS229 6.3 Neurons Networks Gradient Checking

相關推薦