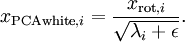CS229 6.7 Neurons Networks whitening
PCA的過程結束後,還有一個與之相關的預處理步驟,白化(whitening)
對於輸入資料之間有很強的相關性,所以用於訓練資料是有很大冗餘的,白化的作用就是降低輸入資料的冗餘,通過白化可以達到(1)降低特徵之間的相關性(2)所有特徵同方差,白化是需要與平滑與PCA結合的,下邊來看如何結合。
對於訓練資料{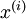 },找到其所有特徵組成的新基U,計算在新基的座標
},找到其所有特徵組成的新基U,計算在新基的座標 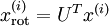 ,這裡
,這裡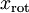 就會消除資料的相關性:
就會消除資料的相關性:
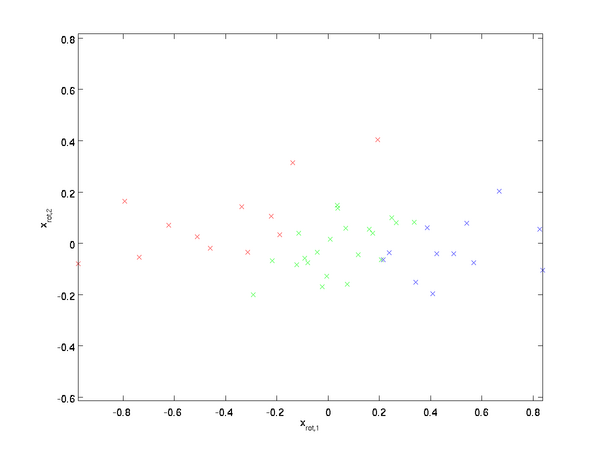
這個資料的協方差矩陣如下:
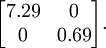
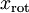 協方差矩陣對角元素的值為
協方差矩陣對角元素的值為 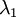 和
和 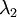 ,且非對角線元素取值為0,課件不同緯度的特徵之間是不相關的,對應的
,且非對角線元素取值為0,課件不同緯度的特徵之間是不相關的,對應的 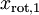
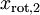 是不相關的,這便滿足白化的第一個要求,降低相關性,下面就要使特徵之間同方差(注意是變化後的特徵同方差
是不相關的,這便滿足白化的第一個要求,降低相關性,下面就要使特徵之間同方差(注意是變化後的特徵同方差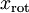 )
)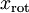 中每個特徵 i 的方差為
中每個特徵 i 的方差為 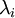 我們可以直接使用
我們可以直接使用 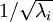 作為縮放因子來縮放每個特徵
作為縮放因子來縮放每個特徵 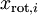 。具體地,我們定義白化後的資料
。具體地,我們定義白化後的資料 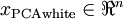 如下:
如下:
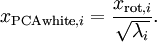
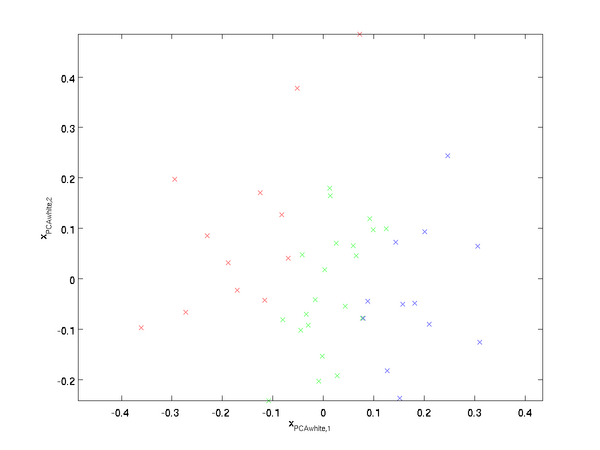
繪製出 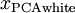 ,可以得到:
,可以得到:
這些資料現在的協方差矩陣為單位矩陣 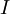 。
。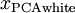 是資料經過PCA白化後的版本:
是資料經過PCA白化後的版本: 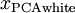 中不同的特徵之間不相關並且具有單位方差。
中不同的特徵之間不相關並且具有單位方差。
白化與降維相結合。 如果你想要得到經過白化後的資料,並且比初始輸入維數更低,可以僅保留 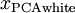
 個成分。當我們把PCA白化和正則化結合起來時(在稍後討論),
個成分。當我們把PCA白化和正則化結合起來時(在稍後討論),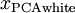 中最後的少量成分將總是接近於0,因而捨棄這些成分不會帶來很大的問題。
中最後的少量成分將總是接近於0,因而捨棄這些成分不會帶來很大的問題。
最後要說明的是,使資料的協方差矩陣變為單位矩陣 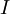 的方式並不唯一。具體地,如果
的方式並不唯一。具體地,如果 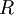 是任意正交矩陣,即滿足
是任意正交矩陣,即滿足 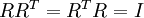 (說它正交不太嚴格,
(說它正交不太嚴格,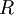 可以是旋轉或反射矩陣), 那麼
可以是旋轉或反射矩陣), 那麼 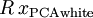 仍然具有單位協方差。在ZCA白化中,令
仍然具有單位協方差。在ZCA白化中,令 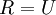 。定義ZCA白化的結果為:
。定義ZCA白化的結果為:
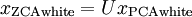
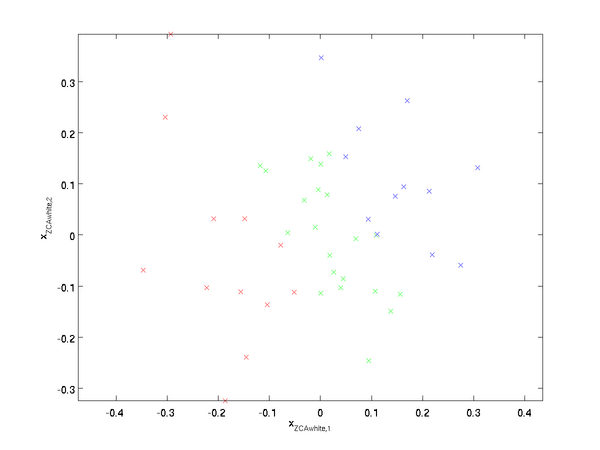
繪製 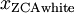 ,得到:
,得到:
可以證明,對所有可能的 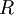 ,這種旋轉使得
,這種旋轉使得 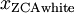
 。
。
當使用 ZCA白化時(不同於 PCA白化),我們通常保留資料的全部 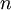 個維度,不嘗試去降低它的維數。
個維度,不嘗試去降低它的維數。
實踐中需要實現PCA白化或ZCA白化時,有時一些特徵值 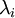 在數值上接近於0,這樣在縮放步驟時我們除以
在數值上接近於0,這樣在縮放步驟時我們除以 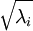 將導致除以一個接近0的值;這可能使資料上溢 (賦為大數值)或造成數值不穩定。因而在實踐中,我們使用少量的正則化實現這個縮放過程,即在取平方根和倒數之前給特徵值加上一個很小的常數
將導致除以一個接近0的值;這可能使資料上溢 (賦為大數值)或造成數值不穩定。因而在實踐中,我們使用少量的正則化實現這個縮放過程,即在取平方根和倒數之前給特徵值加上一個很小的常數 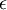 :
:
當  在區間
在區間 ![\textstyle [-1,1]](http://ufldl.stanford.edu/wiki/images/math/8/5/a/85a1c5a07f21a9eebbfb1dca380f8d38.png) 上時, 一般取值為
上時, 一般取值為 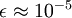 。
。
對影象來說, 這裡加上 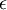 ,對輸入影象也有一些平滑(或低通濾波)的作用。這樣處理還能消除在影象的畫素資訊獲取過程中產生的噪聲,改善學習到的特徵。
,對輸入影象也有一些平滑(或低通濾波)的作用。這樣處理還能消除在影象的畫素資訊獲取過程中產生的噪聲,改善學習到的特徵。