CS229 6.8 Neurons Networks implements of PCA ZCA and whitening
PCA
給定一組二維資料,每列十一組樣本,共45個樣本點
-6.7644914e-01 -6.3089308e-01 -4.8915202e-01 ...
-4.4722050e-01 -7.4778067e-01 -3.9074344e-01 ...

可以表示為如下形式:
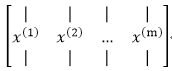
本例子中的的x(i)為2維向量,整個資料集X為2*m的矩陣,矩陣的每一列代表一個數據,該矩陣的轉置X' 為一個m*2的矩陣:

假設如上資料為歸一化均值後的資料(注意這裡省略了方差歸一化),則資料的協方差矩陣Σ為 1/m(X*X'),Σ為一個2*2的矩陣:

對該對稱矩陣對角線化:

這是對於2維情況,若對於n維,會得到一組n維的新基:
 ,且U的轉置:
,且U的轉置:

原資料在U上的投影為用UT*X表示即可:
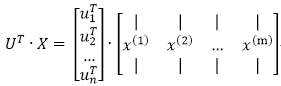
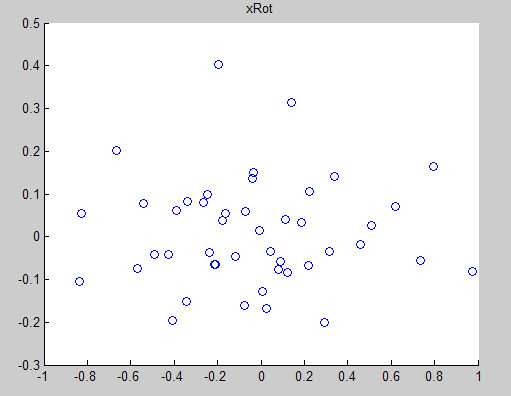
對於二維資料,UT為2*2的矩陣,UT*X會得到2*m的新矩陣,即原資料在新基下的表示XROT,原來的資料對映到這組新基上,便得到可一組在各個維度上不相關的資料,取k<n,把資料對映到 上,便完成的降維過程,下圖為XROT:
上,便完成的降維過程,下圖為XROT:
對基變換後的資料還可以進行還原,比如得到了原始資料 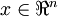 的低維“壓縮”表徵量
的低維“壓縮”表徵量 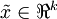 , 反過來,如果給定
, 反過來,如果給定 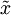 ,我們應如何還原原始資料
,我們應如何還原原始資料  呢?
呢? 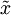
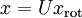 即可。進一步,我們把
即可。進一步,我們把 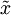 看作將
看作將 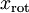 的最後
的最後 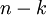 個元素被置0所得的近似表示,因此如果給定
個元素被置0所得的近似表示,因此如果給定 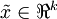 ,可以通過在其末尾新增
,可以通過在其末尾新增 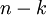 個0來得到對
個0來得到對 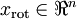 的近似,最後,左乘
的近似,最後,左乘 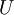 便可近似還原出原資料
便可近似還原出原資料  。具體來說,計算如下:
。具體來說,計算如下:

下圖為還原後的資料:
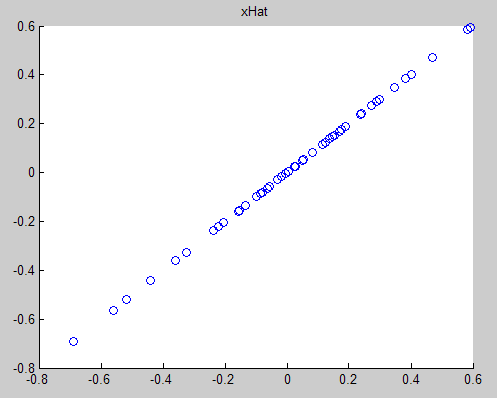
下面來看白化,白化就是先對資料進行基變換,但是並不進行降維,且對變化後的資料,每一個維度上都除以其標準差,來達到歸一化均值方差的目的。另外值得一提的一段話是:
感覺除了層數和每層隱節點的個數,也沒啥好調的。其它引數,近兩年論文基本都用同樣的引數設定:迭代幾十到幾百epoch。sgd,mini batch size從幾十到幾百皆可。步長0.1,可手動收縮,weight decay取0.005,momentum取0.9。dropout加relu。weight用高斯分佈初始化,bias全初始化為0。最後記得輸入特徵和預測目標都做好歸一化。做完這些你的神經網路就應該跑出基本靠譜的結果,否則反省一下自己的人品。
對於ZCA,直接在PCAwhite 的基礎上左成特徵矩陣U即可,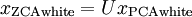
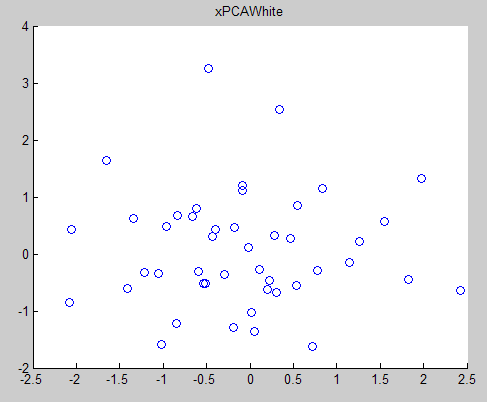

matlab程式碼:

close all %%================================================================ %% Step 0: Load data % We have provided the code to load data from pcaData.txt into x. % x is a 2 * 45 matrix, where the kth column x(:,k) corresponds to % the kth data point.Here we provide the code to load natural image data into x. % You do not need to change the code below. x = load('pcaData.txt','-ascii'); figure(1); scatter(x(1, :), x(2, :)); title('Raw data'); %%================================================================ %% Step 1a: Implement PCA to obtain U % Implement PCA to obtain the rotation matrix U, which is the eigenbasis % sigma. % -------------------- YOUR CODE HERE -------------------- u = zeros(size(x, 1)); % You need to compute this [n m] = size(x); p = mean(x,2);%按行求均值,p為一個2維列向量 %x = x-repmat(p,1,m);%預處理,均值為0 sigma = (1.0/m)*x*x';%協方差矩陣 [u s v] = svd(sigma);%奇異值分解得到特徵值與特徵向量 % -------------------------------------------------------- hold on plot([0 u(1,1)], [0 u(2,1)]);%畫第一條線 plot([0 u(1,2)], [0 u(2,2)]);%第二條線 scatter(x(1, :), x(2, :)); hold off %%================================================================ %% Step 1b: Compute xRot, the projection on to the eigenbasis % Now, compute xRot by projecting the data on to the basis defined % by U. Visualize the points by performing a scatter plot. % -------------------- YOUR CODE HERE -------------------- xRot = zeros(size(x)); % 初始化一個基變換後的資料 xRot = u'*x; %做基變換 % -------------------------------------------------------- % Visualise the covariance matrix. You should see a line across the % diagonal against a blue background. figure(2); scatter(xRot(1, :), xRot(2, :)); title('xRot'); %%================================================================ %% Step 2: Reduce the number of dimensions from 2 to 1. % Compute xRot again (this time projecting to 1 dimension). % Then, compute xHat by projecting the xRot back onto the original axes % to see the effect of dimension reduction % 用投影后的資料還原原始資料 k = 1; % Use k = 1 and project the data onto the first eigenbasis xHat = zeros(size(x)); % 還原原始資料 %[u(:,1),zeros(n,1)]'*x 代表原資料在新基上的前K維的投影,之後的維度為0 %對降維後的資料進行還原:u * xRot = Xhat,Xhat為還原後的資料 xHat = u*([u(:,1),zeros(n,1)]'*x);%n代表資料的維度 % -------------------------------------------------------- figure(3); scatter(xHat(1, :), xHat(2, :)); title('xHat'); %%================================================================ %% Step 3: PCA Whitening % Complute xPCAWhite and plot the results. epsilon = 1e-5; % -------------------- YOUR CODE HERE -------------------- xPCAWhite = zeros(size(x)); % You need to compute this % s為對角陣,diag(s)會返回s主對角線元素組成的列向量 % diag(1./sqrt(diag(s)+epsilon))會返回一個對角陣, % 對角線元素為 -> 1./sqrt(diag(s)+epsilon % 變換後的資料為 : Xrot = u'*x %這樣做對應於Xrot的資料再每個維度除以其標準差 xPCAWhite = diag(1./sqrt(diag(s)+epsilon))*u'*x; % -------------------------------------------------------- figure(4); scatter(xPCAWhite(1, :), xPCAWhite(2, :)); title('xPCAWhite'); %%================================================================ %% Step 3: ZCA Whitening % Complute xZCAWhite and plot the results. % -------------------- YOUR CODE HERE -------------------- xZCAWhite = zeros(size(x)); % You need to compute this xZCAWhite = u*diag(1./sqrt(diag(s)+epsilon))*u'*x; % -------------------------------------------------------- figure(5); scatter(xZCAWhite(1, :), xZCAWhite(2, :)); title('xZCAWhite'); %% Congratulations! When you have reached this point, you are done! % You can now move onto the next PCA exercise. :)View Code
PCA與Whitening與ZCA的一個小實驗:參考自http://deeplearning.stanford.edu/wiki/index.php/Exercise:PCA_and_Whitening

%%================================================================ %% Step 0a: 載入資料 % 隨機取樣10000張圖片放入到矩陣x裡. % x 是一個 144 * 10000 的矩陣,該矩陣的第 k列 x(:, k) 對應第k張圖片 x = sampleIMAGESRAW(); figure('name','Raw images'); randsel = randi(size(x,2),200,1); % A random selection of samples for visualization display_network(x(:,randsel)); %%================================================================ %% Step 0b: 0-均值(Zero-mean)這些資料 (按行) % You can make use of the mean and repmat/bsxfun functions. [n m] = size(x); p = mean(x,1); x = x - repmat(p,1,m); %%================================================================ %% Step 1a: Implement PCA to obtain xRot % Implement PCA to obtain xRot, the matrix in which the data is expressed % with respect to the eigenbasis of sigma, which is the matrix U. xRot = zeros(size(x)); % 新基下的資料 sigma =(1.0/m)*x*x'; [u s v] = svd(sigma); XRot = u'*x; %%================================================================ %% Step 1b: Check your implementation of PCA % 新基U下的資料的協方差矩陣是對角陣,只在主對角線上不為0 % Write code to compute the covariance matrix, covar. % When visualised as an image, you should see a straight line across the % diagonal (non-zero entries) against a blue background (zero entries). % -------------------- YOUR CODE HERE -------------------- covar = zeros(size(x, 1)); % You need to compute this covar = (1./m)*xRot*xRot'; %新基下資料的均值仍然為0,直接計算covariance % Visualise the covariance matrix. You should see a line across the % diagonal against a blue background. figure('name','Visualisation of covariance matrix'); imagesc(covar); %%================================================================ %% Step 2: Find k, the number of components to retain % Write code to determine k, the number of components to retain in order % to retain at least 99% of the variance. % 保留99%的方差比 % -------------------- YOUR CODE HERE -------------------- k = 0; % Set k accordingly for i = i,n: lambd = diag(s)%對角線元素組成的列向量 % 通過迴圈找到99%的方差百分比的k值 for k = 1:n if sum(lambd(1:k))/sum(lambd)<0.99 continue; end %下面是另一種k的求法 %其中cumsum(ss)求出的是一個累積向量,也就是說ss向量值的累加值 %並且(cumsum(ss)/sum(ss))<=0.99是一個向量,值為0或者1的向量,為1表示滿足那個條件 %k = length(ss((cumsum(ss)/sum(ss))<=0.99)); %%================================================================ %% Step 3: Implement PCA with dimension reduction % Now that you have found k, you can reduce the dimension of the data by % discarding the remaining dimensions. In this way, you can represent the % data in k dimensions instead of the original 144, which will save you % computational time when running learning algorithms on the reduced % representation. % % Following the dimension reduction, invert the PCA transformation to produce % the matrix xHat, the dimension-reduced data with respect to the original basis. % Visualise the data and compare it to the raw data. You will observe that % there is little loss due to throwing away the principal components that % correspond to dimensions with low variation. % -------------------- YOUR CODE HERE -------------------- xHat = zeros(size(x)); % You need to compute this %把x對映到U的前k個基上 u(:,1:k)'*x作為Xrot',Xrot'為k*m維的 %補全整個Xrot'中k到n維的元素為0,然後左乘U變回到原來的基下得到Xhat % 首先為了降維做一個基變換,降維後要還原到原來的座標系下,還原後為 %對應的降維後的原始資料 xHat = u*[u(:,1:k)'*x;zeros(n-k,m)]; % Visualise the data, and compare it to the raw data % You should observe that the raw and processed data are of comparable quality. % For comparison, you may wish to generate a PCA reduced image which % retains only 90% of the variance. figure('name',['PCA processed images ',sprintf('(%d / %d dimensions)', k, size(x, 1)),'']); display_network(xHat(:,randsel)); figure('name','Raw images'); display_network(x(:,randsel)); %%================================================================ %% Step 4a: Implement PCA with whitening and regularisation % Implement PCA with whitening and regularisation to produce the matrix % xPCAWhite. epsilon = 0.1; xPCAWhite = zeros(size(x)); % 白化處理 % xRot = u' * x 為白化後的資料 xPCAWhite = diag(1./sqrt(diag(s) + epsilon))* u' * x; figure('name','PCA whitened images'); display_network(xPCAWhite(:,randsel)); %%================================================================ %% Step 4b: Check your implementation of PCA whitening % Check your implementation of PCA whitening with and without regularisation. % PCA whitening without regularisation results a covariance matrix % that is equal to the identity matrix. PCA whitening with regularisation % results in a covariance matrix with diagonal entries starting close to % 1 and gradually becoming smaller. We will verify these properties here. % Write code to compute the covariance matrix, covar. % Without regularisation (set epsilon to 0 or close to 0), % when visualised as an image, you should see a red line across the % diagonal (one entries) against a blue background (zero entries). % With regularisation, you should see a red line that slowly turns % blue across the diagonal, corresponding to the one entries slowly % becoming smaller. % -------------------- YOUR CODE HERE -------------------- % Visualise the covariance matrix. You should see a red line across the % diagonal against a blue background. figure('name','Visualisation of covariance matrix'); imagesc(covar); %%================================================================ % % Step 5: Implement ZCA whitening % Now implement ZCA whitening to produce the matrix xZCAWhite. % Visualise the data and compare it to the raw data. You should observe % that whitening results in, among other things, enhanced edges. xZCAWhite = zeros(size(x)); % ZCA處理 xZCAWhite = u*xPCAWhite; % Visualise the data, and compare it to the raw data. % You should observe that the whitened images have enhanced edges. figure('name','ZCA whitened images'); display_network(xZCAWhite(:,randsel)); figure('name','Raw images'); display_network(x(:,randsel));View Code
參考:http://www.cnblogs.com/tornadomeet/archive/2013/03/21/2973231.html

