CS229 6.2 Neurons Networks Backpropagation Algorithm
今天得主題是BP演算法。大規模的神經網路可以使用batch gradient descent演算法求解，也可以使用 stochastic gradient descent 演算法，求解的關鍵問題在於求得每層中每個引數的偏導數，BP演算法正是用來求解網路中引數的偏導數問題的。
先上一張吊炸天的圖，可以看到BP的工作原理：
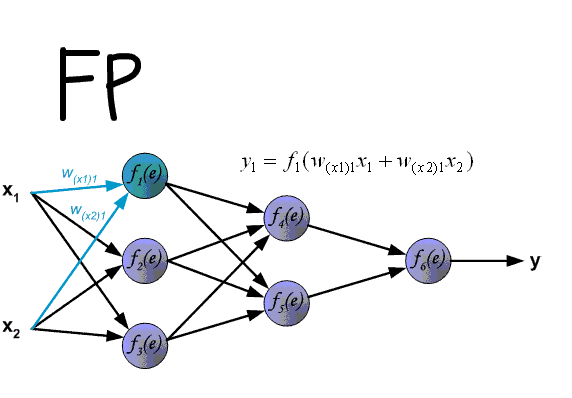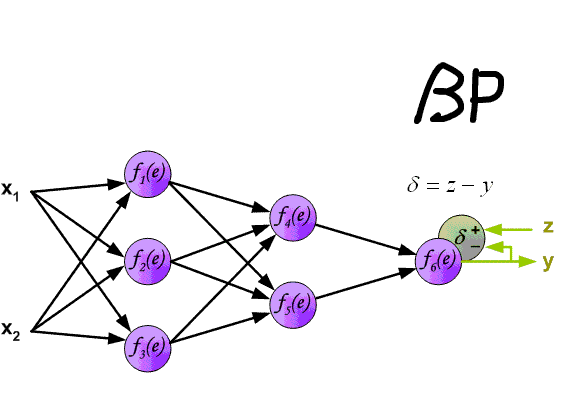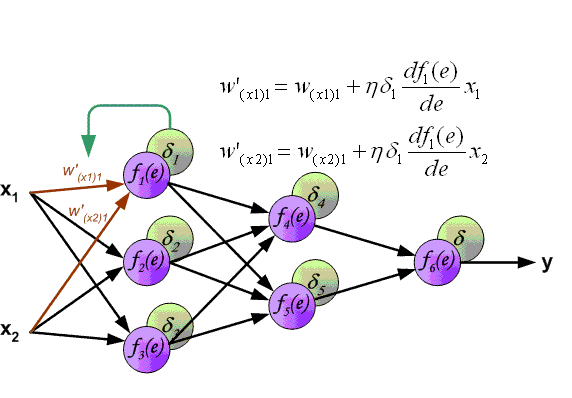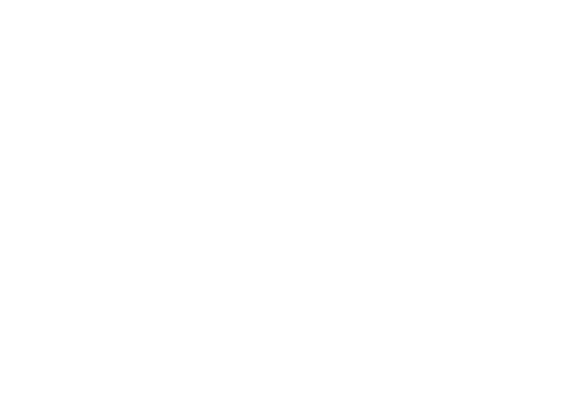
下面來看BP演算法，用m個訓練樣本集合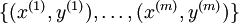
來train一個神經網路，對於該模型，首先需要定義一個代價函式，常見的代價函式有以下幾種：
1）0-1損失函式：（0-1 loss function）
2）平方損失函式：（quadratic loss function）
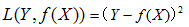
3）絕對值損失函式：（absolute loss function）
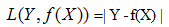
4）負log損失函式（log loss function）
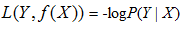
損失函式的意義在於，假設函式（hypothesis function，即模型）的輸出與資料標籤的值月接近，損失函式越小。反之損失函式越大，這樣減小損失函式的值，來求得最優的引數即可，最後將最優的引數帶入帶假設函式中，即可求得最終的最優的模型。
在Neurons Network中，對於一個樣本（x，y），其損失函式可表示為
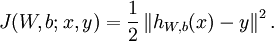
上式這種形式是平方損失函式（注意若採用交叉熵損失則與此損失形式不一樣），對於所有的m個樣本，對於所有訓練資料，總的損失函式為：
![\begin{align}
J(W,b)
&= \left[ \frac{1}{m} \sum_{i=1}^m J(W,b;x^{(i)},y^{(i)}) \right]
+ \frac{\lambda}{2} \sum_{l=1}^{n_l-1} \; \sum_{i=1}^{s_l} \; \sum_{j=1}^{s_{l+1}} \left( W^{(l)}_{ji} \right)^2
\\
&= \left[ \frac{1}{m} \sum_{i=1}^m \left( \frac{1}{2} \left\| h_{W,b}(x^{(i)}) - y^{(i)} \right\|^2 \right) \right]
+ \frac{\lambda}{2} \sum_{l=1}^{n_l-1} \; \sum_{i=1}^{s_l} \; \sum_{j=1}^{s_{l+1}} \left( W^{(l)}_{ji} \right)^2
\end{align}](http://ufldl.stanford.edu/wiki/images/math/4/5/3/4539f5f00edca977011089b902670513.png)
上式中第一項為均方誤差項，第二項為正則化項，用來限制權重W的大小，防止over-fitting，也即貝葉斯學派所說的給引數引入一個高斯先驗的MAP（極大化後驗）方法。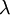
為正則項的引數，用來控制兩項的相對重要性， 比如若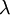很大時，引數W，b必須很小才能使得最終的損失函式J(W，b) 很小。
常見的分類或者回歸問題，都可以用這個損失函式，注意分類時標籤y是離散值，迴歸時對於sigmod函式y為(0,1)之間的連續值。對於tanh為(-1,1)之間的值。
BP演算法的目標就是求得一組最優的W、b ，使得損失函式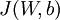 
的值最小
首先將每個引數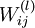 
和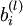 
初始化為一個很小的隨機值（比如說，使用正態分佈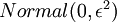 
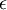設定為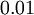 
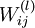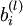），然後使用批梯度下降演算法來優化 和 的值，因為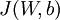 是非凸函式，即存在不止一個極值點，梯度下降演算法很可能會收斂到區域性極值處，但通常效果很不錯（在淺層網路中，比如說三層），需要強調的是要將引數隨機初始化，而不是全部置0，如果所有引數都用相同的值作為初始值，那麼所有隱藏層單元最終會得到與輸入值有關的、相同的函式（也就是說，對於所有hidden unit 
，
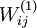都會取相同的值，那麼對於任何輸入 
都會有：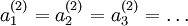
），隨機初始化會消除這種對稱效果。
批梯度下降演算法中，每一次迭代都按照如下公式對引數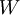 
和
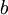進行更新：
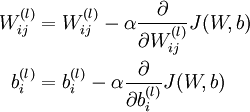
其中J(W，b)包含了所有的樣本，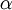
是學習速率，對於多層神經網路，如何計算每一層引數的偏導數是關鍵問題，BP演算法正使用來計算每一項的偏導數的。
首先來看對於單個樣例，引數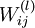 和 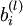的偏導數分別為 
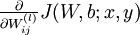和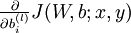 
有了單個樣例的偏導數後，根據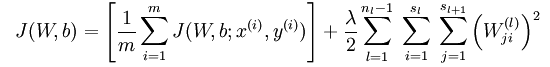
，就可以很好求出損失函式 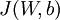的偏導數：
![\begin{align}
\frac{\partial}{\partial W_{ij}^{(l)}} J(W,b) &=
\left[ \frac{1}{m} \sum_{i=1}^m \frac{\partial}{\partial W_{ij}^{(l)}} J(W,b; x^{(i)}, y^{(i)}) \right] + \lambda W_{ij}^{(l)} \\
\frac{\partial}{\partial b_{i}^{(l)}} J(W,b) &=
\frac{1}{m}\sum_{i=1}^m \frac{\partial}{\partial b_{i}^{(l)}} J(W,b; x^{(i)}, y^{(i)})
\end{align}](http://ufldl.stanford.edu/wiki/images/math/9/3/3/93367cceb154c392aa7f3e0f5684a495.png)
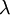並不作用於bais unit b，所以第二個式子中沒有第二項。
先看如下的式子，l+1層的輸入等於l層的加權輸出求和，即
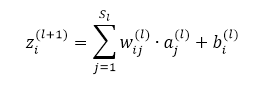
課件hidden layer的輸入z為引數的方程，為了求解對每個樣本中引數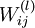 和 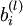的偏導數，可以用根據鏈式求導法則有:
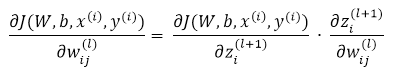
我們把上邊的第一項稱為殘差，有了以上鍊式求導的思想，為了求得各個引數的偏導數，我們需要求得每一層的每個單元的殘差。下面反向傳播演算法的思路：
1）給定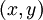 
，我們首先進行“前向傳導”，計算出網路中所有的啟用值，包括 
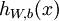的輸出值
2）對第 
層的每個節點 ，計算出其“殘差”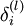 
，該殘差表明節點對最終輸出值的殘差產生多少影響
3）對於最終的輸出節點，直接算出網路產生的啟用值與實際值之間的差距，將這個差距定義為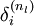 
4）對於隱藏單元，將第 
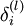層節點的殘差的加權平均值計算 ，這些節點以 
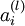作為輸入到 層
下面將給出反向傳導演算法的細節：
1）進行前饋傳導計算，利用前向傳導公式，得到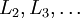 
直到輸出層 
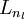的啟用值。
2）對於第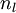 
層（輸出層）的每個輸出單元 ，我們根據以下公式計算殘差：
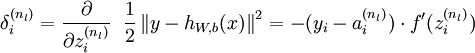
推倒：
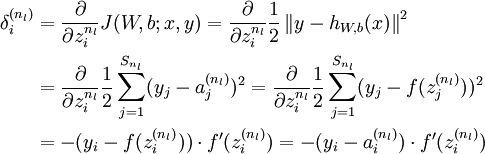
3）對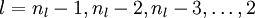 
的各個層，第 層的第 個節點的殘差計算方法如下：
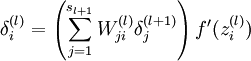
有了最後一層的層差，可以計算前一層的殘差：
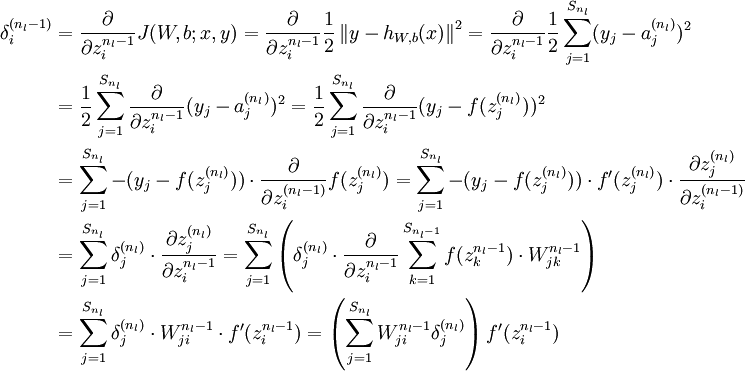
4)將上式中的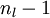 
與 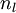的關係替換為 與 的關係，就可以得到：
5)根據鏈式求導法則，計算方法如下：
-
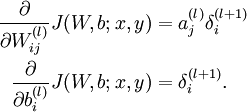
- 其中，第二項的計算公式如下：
-
根據
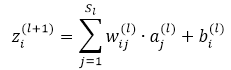，有：
-
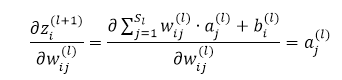
概括一下整個演算法：
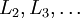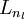1）進行前饋傳導計算，利用前向傳導公式，得到 直到輸出層 的啟用值。
2）對輸出層（第 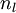層），計算：
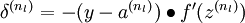
3）對於 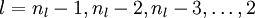的各層，計算：
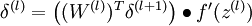
4）計算最終需要的偏導數值：
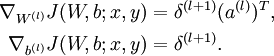
指的注意的是在以上的第2步和第3步中，我們需要為每一個 單元 值計算其 
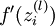。假設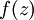 
是sigmoid函式，f'(z)=f(z)*(1-f(z)),並且我們已經在前向傳導運算中得到了 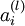。那麼，使用我們早先推匯出的 
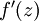表示式，就可以計算得到 
。
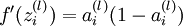經過以上步驟，已經可以求出每個引數的偏導數，下一步就是更新引數，即使得引數沿梯度方向下降，下面給出梯度下降演算法虛擬碼：
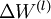是一個與矩陣 
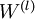維度相同的矩陣，
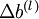是一個與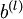 
維度相同的向量。注意這裡“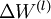”是一個矩陣，而不是“
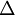與 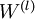相乘”。下面，我們實現批量梯度下降法中的一次迭代：
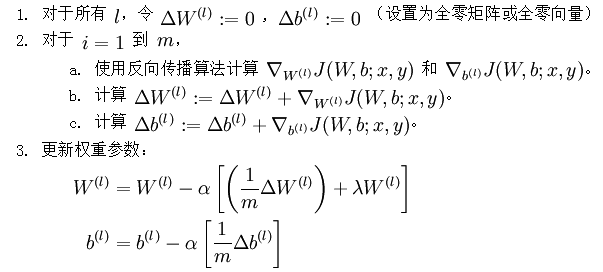
不斷更新W，b的值，直到W，b不再變化為止，即網路達到收斂。