1. 引言

此前的部落格中，我們已經介紹了幾個分類演算法。
k 近鄰演算法
決策樹的構建演算法 – ID3 與 C4.5 演算法
樸素貝葉斯演算法的推導與實踐

本文介紹的是另一個分類演算法 – 邏輯斯蒂迴歸。
他憑藉易於實現與優異的效能，擁有著十分廣泛的使用，他不僅可以進行二分類問題的解決，也可以解決多分類問題，簡單起見，本文我們只討論二分類問題。
它的基本思想是利用一條直線將平面上的點分為兩個部分，即兩個類別，要解決的問題就是如何擬合出這條直線，這個擬合的過程就稱之為“迴歸”。

2. 邏輯斯蒂演算法推導

2.1. 機率函式與 logit 函式

假設一個事件發生的概率是 p，不發生的概率就是 1-p，那麼 p/(1-p) 被稱為事件發生的“機率”。
f§ = p/(1-p) 就是機率函式，舉個簡單的例子，足球賽上，A隊對抗B隊，勝率是 90%，那麼通過幾率函式可以求得 f(0.9) = 9，也就是說，在10場比賽中，A隊可以平均獲勝9場，在實際的生活中，機率函式比概率更為實用。
對機率函式取對數就是 logit 函式：

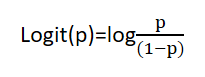
2.2. logistic 函式

我們將上面的例子看作在條件 X = 10 場比賽下，A隊獲勝概率為 90% 時得到的 A 隊獲勝 9 場的特徵結果。
但我們需要解決的是符合一定特徵的樣本其屬於某個類別的概率，這就需要隊上面的函式求反，從而得到 logistic 函式，也稱為 Sigmoid 函式：

2.3. 繪製 Sigmoid 函式圖

通過下面的 python 程式碼我們可以繪製出 Sigmoid 函式的函式圖：

import matplotlib.pyplot as plt
import numpy as np
 
 
def sigmoid(z):
    return 1.0/(1.0 + np.exp(-z))
 
 
if __name__ == '__main__':
    z=np.arange(-6, 6, 0.05)
    plt.plot(z, sigmoid(z))
    plt.axvline(0.0, color='k')
    plt.axhline(y=0.0, ls='dotted', color='k')
    plt.axhline(y=1.0, ls='dotted', color='k')
    plt.axhline(y=0.5, ls='dotted', color='k')
    plt.yticks([0.0, 0.5, 1.0])
    plt.ylim(-0.1, 1.1)
    plt.xlabel('z')
    plt.ylabel('$\phi (z)$')
    plt.show()

3. 代價函式

假設我們的樣本 x 具有 x1、x2、x3 。。。xn 等多個特徵，通過新增係數 θ 可以得到下面的公式：

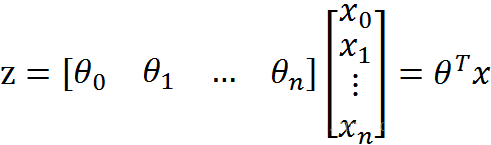
從而得到：

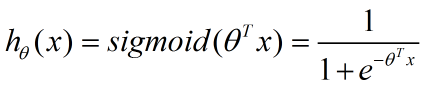
因為我們要解決二分類問題，所以我們只關心發生和不發生的概率，也就是 y=0 與 y=1 的解：

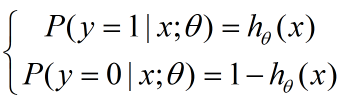
因為 y 只有 0 和 1 兩個取值，我們可以通過下面函式將上面兩個函式整合在一起：

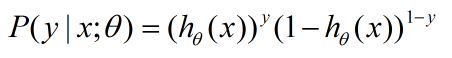
這個函式就是代價函式。

4. 極大似然估計

有了代價函式，我們只要找到所有的 θ 使得對於我們的所有樣本都能成立就可以了，這個找 θ 的過程就是極大似然估計。
極大似然估計的目的就是利用已知的樣本結果，反推最有可能（最大概率）導致這樣結果的引數值，從而將概率密度估計問題轉化為引數估計問題。
但他有一個明顯的前提需要保證：訓練樣本的分佈能代表樣本的真實分佈。
p(x1, x2, x3, …, xn|θ) 被稱為 {x1, x2, x3, …, xn} 的 θ 的似然函式。
在假設全部特徵 x1, x2, x3 …, xn 均為獨立特徵的前提下，我們可以得到：

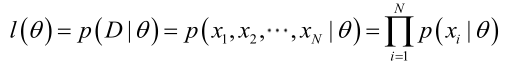
5. 梯度上升法求解極大似然函式

5.1. 準備求解

讓 l(θ) 函式獲得最大值的 θ 值就是我們想要的值。

正如上一篇日誌中所寫的，連續積運算通過對數轉換為累加是數學中的常用方法，因此我們對上面函式兩邊求 log。

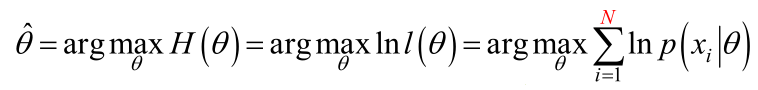
假設函式連續且任一點可導，那麼，要計算一個函式結果取到極值時的引數值，我們通常只需要讓函式的導數為 0 即可計算出函式取極值時的引數值。

我們定義梯度因子為：

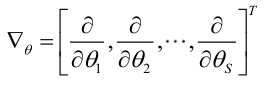
那麼我們希望求解：

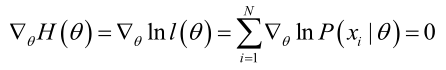
這個函式的直接求解太過複雜，因此不能直接求解，有幾種方法可以通過迭代的方式得到近似的估計值，例如牛頓-拉菲森迭代方法。
本文我們介紹另一種迭代方法 – 梯度上升法，梯度上升演算法和牛頓迭代相比更加易於理解，但收斂速度慢，因為梯度上升演算法是一階收斂，而牛頓迭代屬於二階收斂。

5.2. 梯度上升法

梯度上升法的原理是像爬坡一樣，一點一點的向上爬，等到爬到山頂，那就已經非常接近我們的極值點了。
也就是說，每次比較上一次的函式值和本次的函式值，如果本次的函式值大於上一次的函式值，說明正處於上升階段，否則說明已經進入了下降階段，那麼上次的點就是極值點。

但是這裡有一個上升步長的問題，如果我們步子邁得太大，那麼很容易就越過山頂了，最後只把半山腰上的某個點認成了極值點，而如果步子邁得太小，那麼就會耗費更加大量的時間去不斷地爬坡。
根據我們的經驗，函式的導數是隨著我們接近極值點而逐漸減小的，所以我們只要讓步長正比於函式的導數，就可以讓我們的步子隨著極值點的接近越來越小，因此我們定義上升函式：

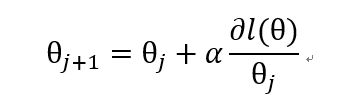
α 是步長係數。

5.3. 求解 l(θ) 的導數

現在，我們只要求出 l(θ) 導數帶入上面的公式就可以利用梯度上升演算法，求解 l(θ) 的極大值了。
接下來就是數學推導過程了：

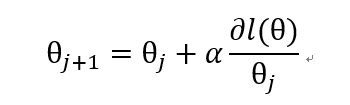
通過新增項的方法，我們可以將求導問題歸類為三部分的求解：

• 第一部分

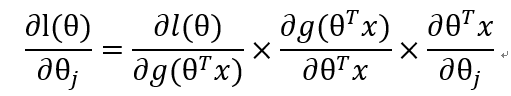
• 第二部分
  根據：

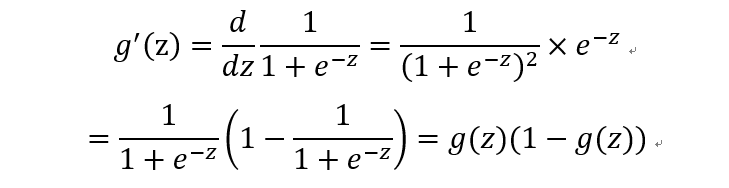
可得：

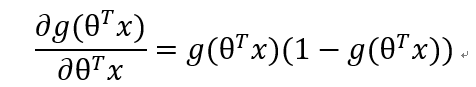
• 第三部分

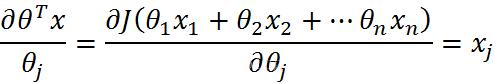
綜上：

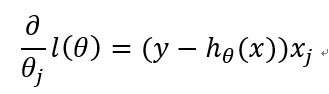
從而得到梯度上升迭代公式：

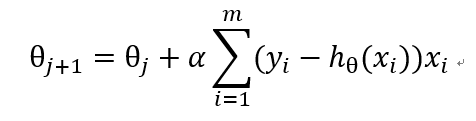
6. 參考資料

https://en.wikipedia.org/wiki/Maximum_likelihood_estimation。
https://en.wikipedia.org/wiki/Gradient_descent。
https://zlatankr.github.io/posts/2017/03/06/mle-gradient-descent。
https://blog.csdn.net/c406495762/article/details/77723333。
https://blog.csdn.net/zengxiantao1994/article/details/72787849。
https://blog.csdn.net/sinat_29957455/article/details/78944939。
https://blog.csdn.net/amds123/article/details/70243497。
https://blog.csdn.net/gwplovekimi/article/details/80288964。
https://www.cnblogs.com/HolyShine/p/6395965.html。