隨機數生成器與線性同餘法產生隨機數

1、隨機數生成器與/dev/random：

隨機數生成器，顧名思義就是能隨機產生數字，不能根據已經產生的數預測下次所產生的數的“器”（器存在軟體與硬體之分），真正的隨機數生成器其產生的隨機數具有隨機性、不可預測性、不可重現性。

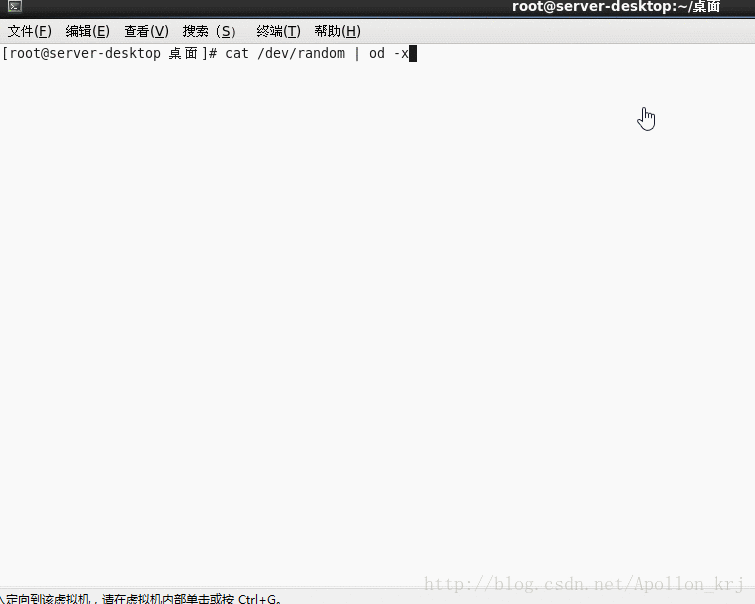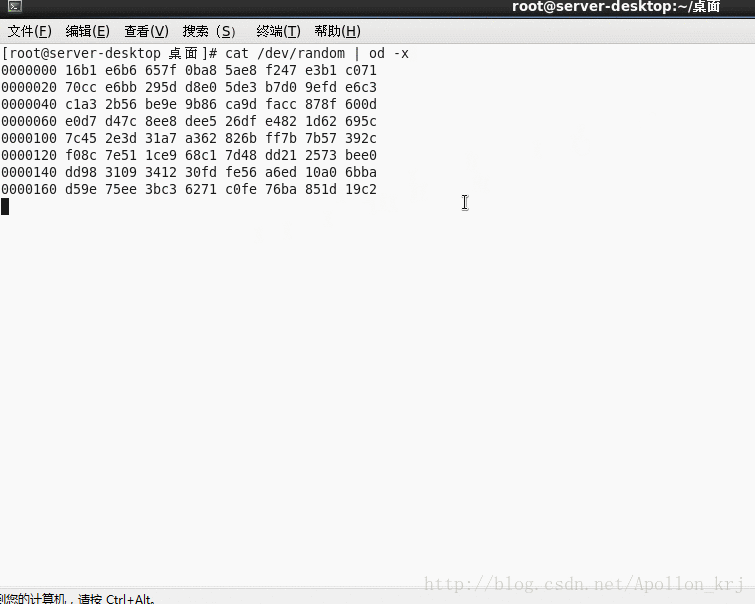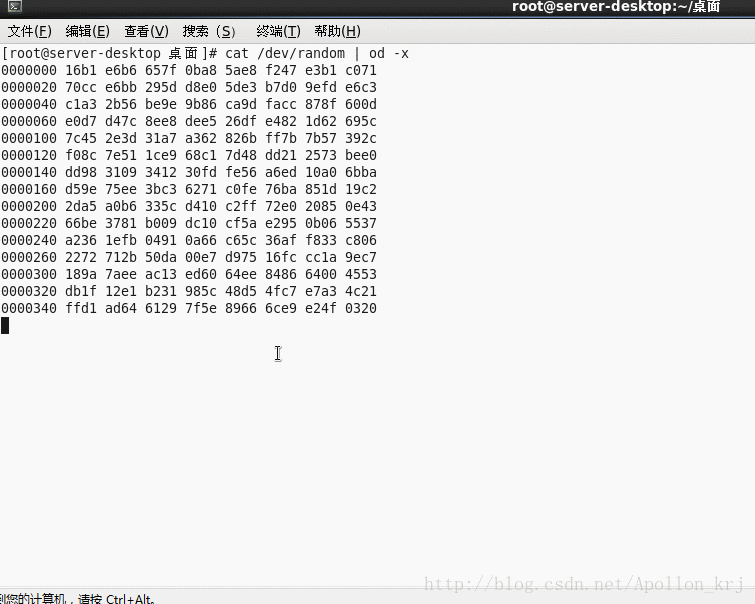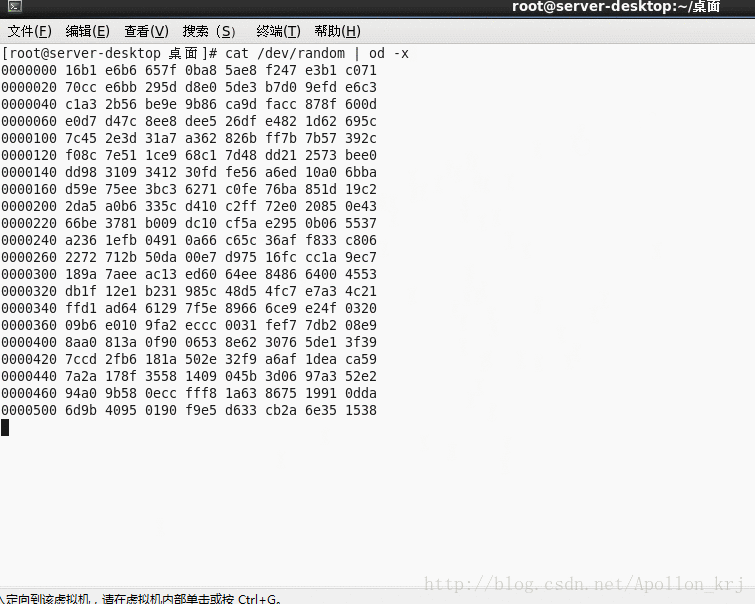
什麼是真正的隨機數生成器？指的是由感測器採集裝置外部溫度、噪聲等不可預測的自然量產生的隨機數。比如Linux的/dev/random裝置檔案其根據裝置中斷（鍵盤中斷、滑鼠中斷等）來產生隨機數，由於滑鼠的操作（移動方向、點選）是隨機的、不可預測的也是不可重現的，所以產生的隨機數是真隨機數。/dev/random即所謂的隨機數池，當通訊過程（如https安全套接層SSL）需要加密金鑰時，就從隨機數池中取出所需長度的隨機數作為金鑰，這樣的金鑰就不會被攻擊者（Attacker）猜測出。但是由於/dev/random是採集系統中斷來生成隨機數的，所以在無系統中斷時，讀取/dev/random是處於阻塞狀態

cat讀取/dev/radom測試效果.gif

在Linux上還存在隨機數生成器/dev/urandom，而讀取該隨機數池是不會阻塞的，因為其不受實時變化的因素影響，所以/dev/urandom是一個偽隨機數生成器，而C語言的rand()庫函式所產生的隨機數也是偽隨機數。/dev/random與/dev/urandom的區別在於一個阻塞一個非阻塞，一個更安全一個較安全。對於/dev/random來說，如果需要的隨機數長度小於隨機數池中的隨機數，則直接返回獲取到的隨機數，並且池中的隨機數長度減去獲取長度，如果要獲取的隨機數長度大於池中已有的長度，則獲取的程序處於阻塞狀態等待新的生成的隨機數部分注入池中。

2、偽隨機數生成器：

所謂偽隨機數生成器，指的是其生成的數在特定條件下是具有真隨機數的特性的。偽隨機數採用“軟體演算法+隨機數種子”的方式來實現，演算法一般不保密，而種子則必須要保密，其基本結構如下所示：

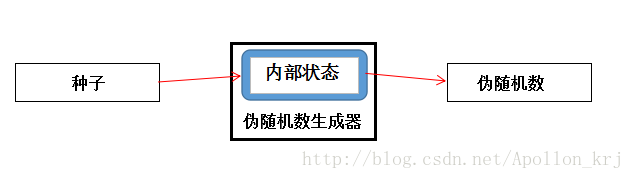
（圖1）偽隨機數生成器結構圖

所謂種子類似於密碼演算法中的加密金鑰，不同的種子（金鑰）對應不同的隨機數（密文）。內部狀態指的是每一個狀態下，隨機數生成器中的數值狀態，初始狀態則是由種子來決定的。而將內部狀態計算偽隨機數的方法和內部狀態改變的方法組合起來就是偽隨機數生成器的演算法。

3、rand()函式採用的隨機數生成器演算法：

rand()函式是C語言的庫函式，其產生隨機數的演算法為線性同餘法（linear congruential method）

（圖2）線性同餘法演算法結構圖

其基本虛擬碼為：

M = 正整數;
A = 大於0且小於M的正整數;
C = 大於0且小於M的正整數;
內部狀態 = 種子seed;
while(true){
    偽隨機數 = (A × 內部狀態 + C) mod M;
    內部狀態 = 偽隨機數;
    輸出偽隨機數;
}

對於rand()函式來說，其種子seed常用當前時間戳（srand(time(NULL));）。由於對M取餘，所以該隨機數具有周期性，而M的大小決定了週期長短（M-1），而A和C也會影響週期（使得週期小於M-1），A、C、M的取值決定了產生的數是否具有不可預測性。比如當A=1，C=0，M=7時，產生的數只能是seed%7，週期為1。不具備隨機數特徵。所以A、C、M的選取是否得當十分重要（關於A、C、M、seed的取值如何才能比較好，可參考http://blog.csdn.net/memray/article/details/8932518）。

4、rand()與srand()函式程式碼實現：

srand()函式只是用種子初始化內部狀態，因為srand()與rand()中都會對內部狀態進行改變，所以內部狀態的變數需要定義為靜態全域性變數。

VC中對於rand()的實現為：

//檔案位置C:\Program Files\Microsoft Visual Studio\VC98\CRT\SRC\rand.c
#include <cruntime.h>
#include <mtdll.h>
#include <stddef.h>
#include <stdlib.h>

#ifndef _MT
//MT為multithread(多執行緒)的縮寫
//如果不是多執行緒則定義holdrand為內部狀態變數
static long holdrand = 1L;
#endif  /* _MT */


void __cdecl srand (unsigned int seed)
{
    #ifdef _MT
        _getptd()->_holdrand = (unsigned long)seed;//執行緒中分別初始化
    #else
        holdrand = (long)seed;
    #endif
}

/**************************************************
其中：A=214013、C=2531011、M=65536（2^16）
在這裡C=7 x 17 x 21269因此C與M是互為質數的，但是M比A和C都小，所以產生的隨機數週期小於M
holdrand最初是seed，經過rand()之後holdrand就變為(holdrand × A + C) mod M
***************************************************/

int __cdecl rand (void)
{
    #ifdef _MT
        _ptiddata ptd = _getptd();//在不同執行緒中獲取各自的內部狀態，避免混淆
        return( ((ptd->_holdrand = ptd->_holdrand * 214013L + 2531011L) >> 16) & 0x7fff );
    #else
        return(((holdrand = holdrand * 214013L + 2531011L) >> 16) & 0x7fff);
    #endif
}

線性同餘法只是常用在程式語言函式庫中產生隨機數（VC中的庫函式是比較簡單的版本，但是比較容易理解，glibc-2.21中的實現更為複雜，可參考http://ftp.gnu.org/gnu/glibc/glibc-2.21.tar.gz中glibc-2.21/stdlib/目錄下的rand.c、rand_r.c和random.c、random_r.c），但是不適用於加密金鑰的生成。因為當被攻擊者獲取到某些隨機數之後，其種子seed以及A、C、M都會被反向計算出來，即有可能根據以往隨機數預測出之後還未產生的隨機數。而使用單向雜湊函式法（單向性作為不可預測的基礎）、密碼法（保密性作為不可預測的基礎）、ANSI X9.17方法（PGP加密軟體使用的偽隨機數生成器演算法，也是採用加密方式來確保隨機數的不可預測性）的隨機數生成器來確保隨機數的不可預測性。

參考資料：《圖解密碼技術》

轉自：https://blog.csdn.net/Apollon_krj/article/details/78718598