我們先來看，要求一個整數的 n 次冪，普通的方法的話，是不是需要乘以 n 次這個數？這裡如果冪次非常大的話，肯定會非常耗時，所以有超時的危險，也是有很多卡時間的題的，所以這裡就牽涉到一個快速冪的思想：

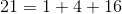
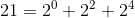
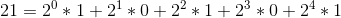
所謂快速冪，就是快速求冪次。我們知道，所有的數字，都可以用二進位制來表示對吧，比如 21 ，它的二進位制數字為 10101 ，也就是他可以分成 ，也就是，也就是二進位制數從最後一位，權值為 1，到最高位權值為 16，可以看到如下情況：，所以這個數的二進位制數的各個位上的數字，如果為 1，就加上這個位的權值，如果不為 1，就不加。

然後介紹一下 ‘&’ 這個符號的意義，這個符號就是將對應二進位制位對齊，然後同一位上都為 1

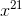
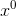
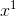
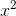
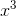
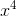
所以我們可以用 & 來取出最後一位的數字，然後用 >> 右移來一步一步進行提取，然後如果最後一位上的數字為 1，則為真，否則為假。而我們一般分解的數字是冪次的數字，也就是如果要求我們分解的是 21，然後權值就會變成，，，，，所以如果判斷為真（最後一位為1）則乘以對應的權值，如果判斷為假，則不乘。

注意：不管當前位是不是 1，都要權值都要自乘，因為權值要一直改變。

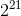
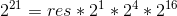
所以當我們需要求的時候，我們將它分為，此處 res = 1，所以只需要計算 3 + 4（自乘） 次乘法，而不是 21 次。

普通版程式碼：

/**普通演算法*/
#define ll long long int
ll power1(ll a, ll b) ///a為底數,b為冪次
{
    ll res = 1;
    for(ll i = 1; i <= b; i++) ///乘以b次底數
    {
        res *= a;
    }
    return  res;
}

快速冪演算法：

/**快速冪優化後演算法*/
#define ll long long int
ll power2(ll a, ll b) ///a為底數,b為冪次
{
    ll res = 1; ///res為最終結果
    a %= c; ///a為權值
    while (b)
    {
        if (b & 1) ///判斷最後一位
            res = res * a;
        a = a * a; ///a自乘
        b >>= 1; ///b應當右移一位
    }
    return res;
}

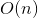
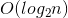
優化後演算法時間複雜度可以從變成，當資料大的時候，優化其實是特別明顯的。

OVER！