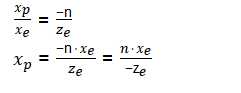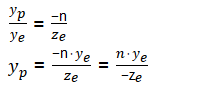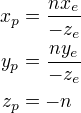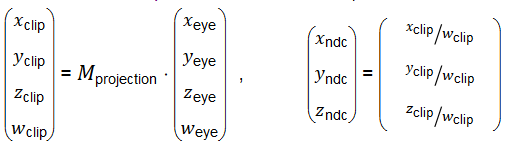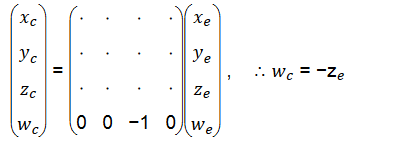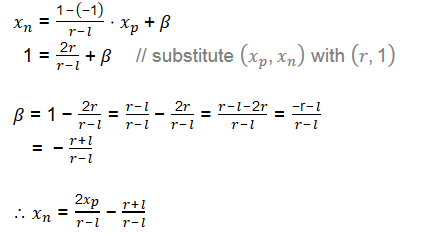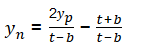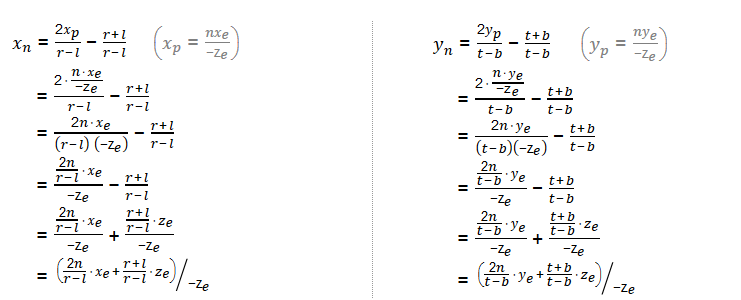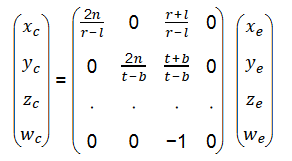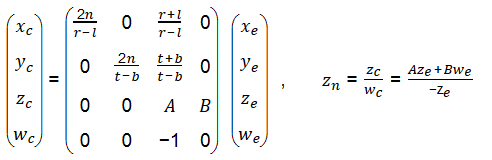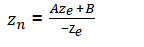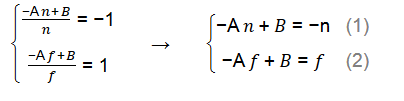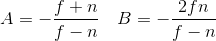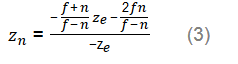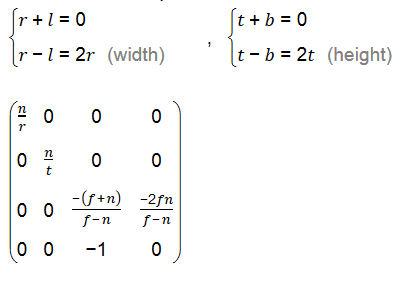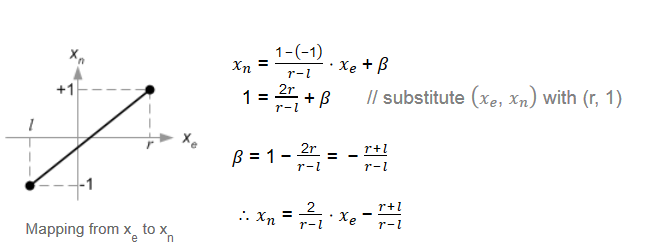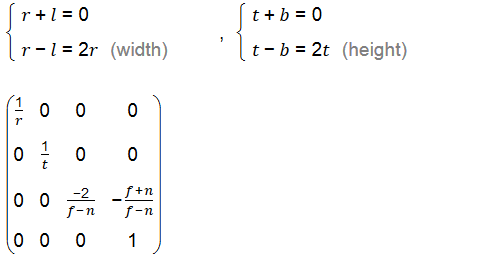opoengl 投影矩陣的推導
原文:http://blog.csdn.net/wangdingqiaoit/article/details/39010077
OpenGL學習腳印: 投影矩陣的推導
寫在前面
本節內容翻譯和整理自http://www.songho.ca songho的部落格《OpenGL Projection Matrix》內容,以供自己和初學者熟悉投影矩陣推導過程。
通過本節,你可以瞭解到:
- 投影矩陣計算的階段
- 透視投影和正交投影的矩陣推導
1.概覽
計算機螢幕是2維的,OpenGL渲染的3D場景必須以2D形式的影象投影到螢幕上。GL_PROJECTION 矩陣就是用來設定投影變換的。首先,它將所有頂點從眼座標(
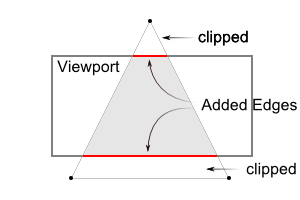
一個由視錐裁剪的三角形
因此,我們要記住,裁剪(視錐剔除frustum culling)和NDC轉換都整合到了GL_PROJECTION 矩陣。接下來的部分描述了怎麼樣通過left, right, bottom, top, near and far 這6個界限引數來構造投影矩陣。
注意:
視錐剔除是在裁剪座標系中進行的,並且恰好在透視除法之前進行。裁剪座標xc, yc 和 zc 通過與wc比較來進行測試。 如果某個座標值比Wc小或者比Wc大,那麼這個頂點將被丟棄。然後,OpenGL會重新在裁剪進行的地方構造多邊形的邊緣。
補充內容:
實際上,眼座標系下座標在乘以投影矩陣後,裁剪測試和透視除法都是由GPU來執行的。而後面這兩個過程處理的裁剪座標系資料都是由投影矩陣變換的。
1. 裁剪測試也即視錐剔除
-Wc < Xc,Yc,Zc < Wc
2. NDC透視除法
Xn = Xc / Wc Yn = Yc / Wc Zn = Zc / Wc
這裡需要注意的是,我們在構造16個引數的投影矩陣的同時,不僅要考慮到裁剪,還要考慮到透視除法的過程。這樣,最終的NDC座標才會滿足:
-1 < Xn,Yn,Zn < 1
2.透視投影
在透視投影中,在眼座標下截頭椎體(a truncated pyramid frustum)內的3D點被對映到NDC下一個立方體中;x座標從[l,r]對映到[-1,1],y座標從[b,t]對映到[-1,1],z座標從[n,f]對映到[-1,1]。
注意:
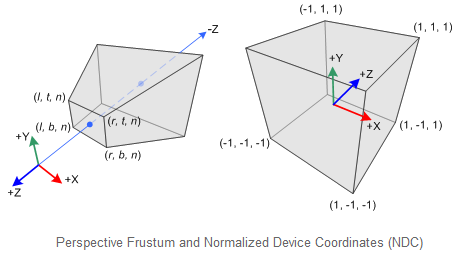
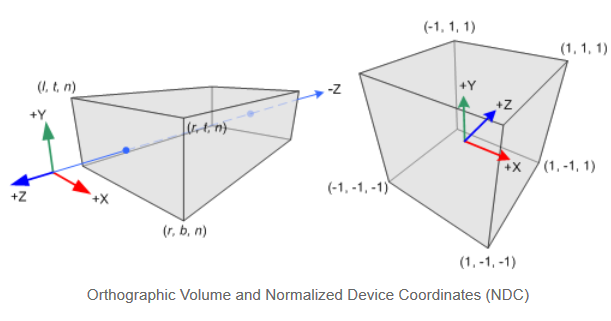
眼座標系使用右手座標系,而NDC使用左手座標系。這就是說,眼座標系下,在原點處的照相機朝著-Z軸看去,但是在NDC中它朝著+Z軸看去。因為glFrustum() 僅接受正的near和far距離,我們在構造GL_PROJECTION 矩陣時,需要取其相反數。眼座標系和NDC座標系如下圖所示:
在OpenGL中,眼座標下3D點被投影到近裁剪面(即投影平面)。下圖展示了眼座標系下點(xe, ye, ze) 如何投影到近裁剪面上的 (xp, yp, zp) 的。(左側是視錐的俯檢視,右側是視錐的側檢視,拿出右手構成右手座標系,然後比劃比劃就出來了)
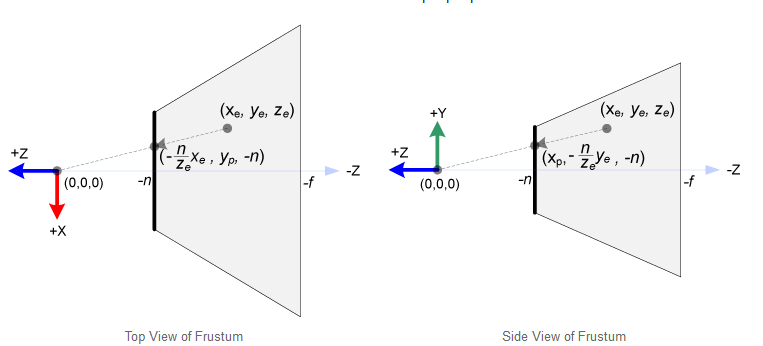
根據三角形的相似性,由俯檢視可得出:
由側檢視可以得出:
補充: xp 和yp其實是一箇中間值,我們要找的是(Xc, Yc, Zc)和 (Xn, Yn, Zn)之間的關係,但是可以利用:
這一關係做過渡,後面利用xp和yp,對映到NDC中xn和yn的線性關係就利用到了 xp 和yp。這一點很重要。
注意,這裡 xp 和yp 都依賴於ze,他們與 -ze成反比。換句話說,他們都被 -ze相除。這個事構造GL_PROJECTION 矩陣最初的線索。在眼座標通過乘以 GL_PROJECTION 來轉換時,裁剪座標系仍然是一個齊次座標系。通過對裁剪座標進行透視除法得到最終的NDC座標。下圖解釋了這個過程:
因此我們可以把裁剪座標系下的w分量設為-ze,那麼GL_PROJECTION矩陣第4行變為(0, 0, -1, 0),如下圖(求出了投影矩陣第4行):
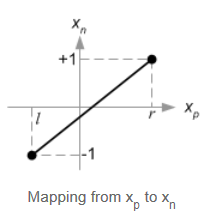
下現在我們把xp和yp,對映到NDC中xn和yn,他們之間是線性關係: [l, r] ⇒ [-1, 1]和[b, t] ⇒ [-1, 1].
線性關係如下圖所示:
則可以推匯出:
細節部分有刪節,這個推導過程使用的就是簡單的y=kx+b線性關係推導,同理利用[b, t] ⇒ [-1, 1]可推得:
將上面的 xp 和yp帶入求得:
注意這裡Xn和Yn已經是NDC中的座標了,通過這兩個座標可以求出GL_PROJECTION 的前兩行來,書寫如下(求出了投影矩陣第1,2,4行):
現在怎麼求出第3行呢?
找出zn與找出xn和yn不同,因為 ze總是被投影近裁剪面-n上。但是我們需要唯一的Z值進行裁剪和深度測試。另外,我們還能夠unproject即反向變換(inverse transform)。因為Z值不依賴於x或者y,因此我們借用w分量來找出 zn 和 ze之間的關係。
因此我們可以這樣指定第3行:
在眼座標下We等於1,因此上式變為:
我們使用(ze, zn)的關係(-n, -1)和 (-f, 1)來求解出係數A,B;
細節部分有刪節,使用消元法即可求出:
我們求出了A和B,那麼ze和zn關係如下式:
最終的投影矩陣如下式:
這個公式對應的是一般的視錐,如果視錐是對稱的,即r = -l ,t= -b,那麼有:
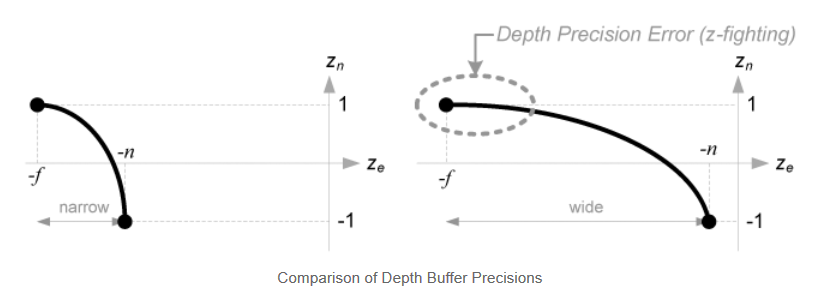
z-fighting
在繼續之前,我們來看看錶示ze和zn關係的式3.這是一個有理函式,並且ze和zn之間不是線性關係。這意味著,在近裁剪面的精度很高,而遠裁剪面則很小。如果[-n, -f]範圍變得大寫,就會引起深度精度問題,即z-fighting。在遠裁剪面附近,ze的小變化根本不影響zn值。近裁剪面和遠裁剪面之間的n和f舉例,應該儘可能小,來減少深度快取的精度問題。可參考下圖來幫助理解。
3.正交投影
構造正交投影的矩陣簡單很多。所有的是眼座標下xe, ye 和ze,都被線性的對映到NDC中。我們需要做的就是講長方體視景體縮放為規範視見體,然後移動到原點。如下圖所示:
以xe和xn之間對映關係為例,[l,r]=>[-1,1],則可以推導如下:
y,z也有類似推導,這裡省略,最後得出投影矩陣為:
如果視錐是對稱的話,即r = -l ,t= -b的話,則可以簡化為:
到這裡透視投影和正交投影矩陣推導完畢。