1.基本概念

多項式迴歸(Polynomial Regression)是研究一個因變數與一個或多個自變數間多項式的迴歸分析方法。如果自變數只有一個 時，稱為一元多項式迴歸；如果自變數有多個時，稱為多元多項式迴歸。 

1.在一元迴歸分析中，如果依變數y與自變數x的關係為非線性的，但是又找不到適當的函式曲線來擬合，則可以採用一元多項式迴歸。 

2.多項式迴歸的最大優點就是可以通過增加x的高次項對實測點進行逼近，直至滿意為止。 

3.事實上，多項式迴歸可以處理相當一類非線性問題，它在迴歸分析 中佔有重要的地位，因為任一函式都可以分段用多項式來逼近。

2.例項

我們在前面已經根據已知的房屋成交價和房屋的尺寸進行了線 性迴歸，繼而可以對已知房屋尺寸，而未知房屋成交價格的例項進行了成 交價格的預測，但是在實際的應用中這樣的擬合往往不夠好，因此我們在 此對該資料集進行多項式迴歸。

目標：對房屋成交資訊建立多項式迴歸方程，並依據迴歸方程對房屋價格進行預測 

import matplotlib.pyplot as plt
import numpy as np
from sklearn import  linear_model
#匯入線性模型和多項式特徵構造模組
from sklearn.preprocessing import  PolynomialFeatures

datasets_X =[]
datasets_Y =[]
fr =open('prices.txt','r')
#一次讀取整個檔案。
lines =fr.readlines()
#逐行進行操作，迴圈遍歷所有資料
 
for line in lines:
    #去除資料檔案中的逗號
items =line.strip().split(',')
    #將讀取的資料轉換為int型，並分別寫入datasets_X和datasets_Y。
datasets_X.append(int(items[0]))
    datasets_Y.append(int(items[1]))
#求得datasets_X的長度，即為資料的總數。
length =len(datasets_X)
#將datasets_X轉化為陣列， 並變為二維，以符合線性回 歸擬合函式輸入引數要求
datasets_X= np.array(datasets_X).reshape([length,
 
1])
#將datasets_Y轉化為陣列
datasets_Y=np.array(datasets_Y)

minX =min(datasets_X)
maxX =max(datasets_X)
#以資料datasets_X的最大值和最小值為範圍，建立等差數列，方便後續畫圖。
X=np.arange(minX,maxX).reshape([-1,1])
#degree=2表示建立datasets_X的二 次多項式特徵X_poly。
poly_reg =PolynomialFeatures(degree=2)
X_ploy =poly_reg.fit_transform(datasets_X)
lin_reg_2=linear_model.LinearRegression()
lin_reg_2.fit(X_ploy,datasets_Y)

#查看回歸方程係數
print('Cofficients:',lin_reg_2.coef_)
#查看回歸方程截距
print('intercept',lin_reg_2.intercept_)
plt.scatter(datasets_X,datasets_Y,color='red')
plt.plot(X,lin_reg_2.predict(poly_reg.fit_transform(X)),color='blue')
plt.xlabel('Area')
plt.ylabel('Price')
plt.show()

執行結果：

Cofficients: [0.00000000e+00 4.93982848e-02 1.89186822e-05]
intercept 151.8469675050044

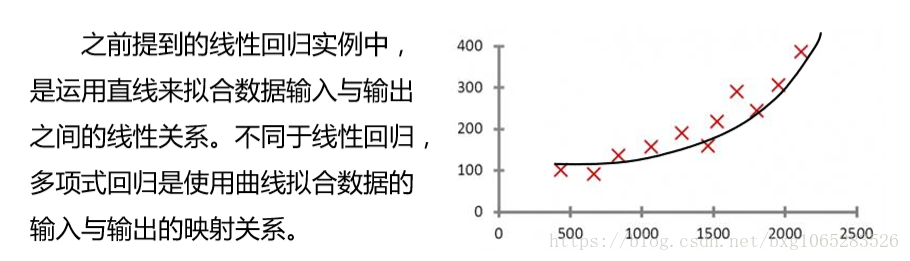
通過多項式迴歸擬合的曲線與 資料點的關係如下圖所示。依據該 多項式迴歸方程即可通過房屋的尺 寸，來預測房屋的成交價格。