折線分割平面

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 20315    Accepted Submission(s): 13928


Problem Description 我們看到過很多直線分割平面的題目，今天的這個題目稍微有些變化，我們要求的是n條折線分割平面的最大數目。比如，一條折線可以將平面分成兩部分，兩條折線最多可以將平面分成7部分，具體如下所示。

Input 輸入資料的第一行是一個整數C,表示測試例項的個數，然後是C 行資料，每行包含一個整數n(0<n<=10000),表示折線的數量。


Output 對於每個測試例項，請輸出平面的最大分割數，每個例項的輸出佔一行。


Sample Input 2 1 2
Sample Output 2 7
Source  

         對於遞推問題 ，無非就是一個找規律，遞推遞推，顧名思義就是從前往後一次的推導。因此，遞推問題，

通常都能夠有兩種解法，一種是求其通項公式，某些的遞推題能夠求的它的遞推公式，另外一種則是利用n-1項的或更多項推導第n項與其他項的關係，從而推匯出遞推公式。（顯然後者更跟遞推問題的本意符合，當然，後者的方法也是解答遞推問題的主要方法。）

        本題的解答以上兩種方法都是可以解答出來的。
 
        下面我們就來推導一下的他們的解題公式（先附上兩條折線和三條折線的畫法）

兩條折線的畫法（有多種畫法，這裡就畫兩種畫法（最為對比推理），要求最多故需要的是圖二的畫法，也是原題給出的圖）


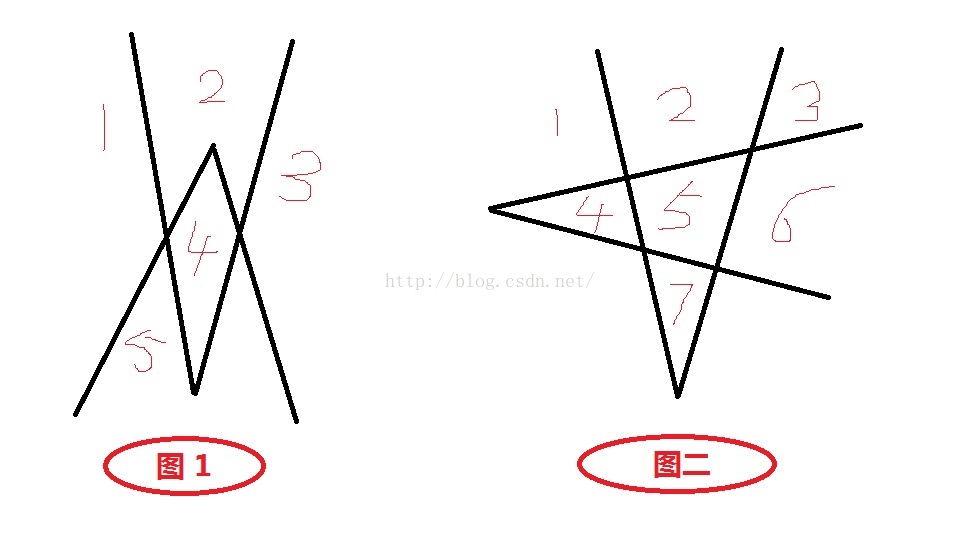
以下是三條折線的畫法（當然三條折線的畫法有很多，這裡就只給大家畫出來正確的一種）

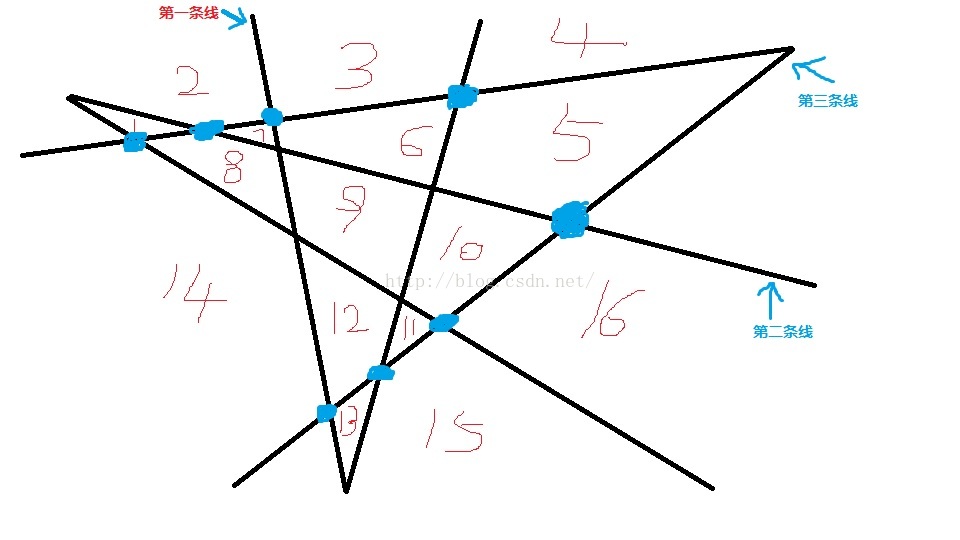
          這裡我給大家推導以下遞推公式的推導步驟：
         上面看到了兩條折線 和三條折線的畫法，我們先來考慮以下兩條折線的畫法，同樣是兩條折線為什麼圖二的就比圖一的要多呢，我們這裡仔細的分析以下兩個圖的不同，經過觀察，不難發現，圖二的交點比圖一的交點多了兩個，那是不是這個原因呢？回答是當然！那麼問題又來了  交點的數目與分割的數量的增加有關係麼？回答仍然是當然！那麼交點數目與分割的數量到底有什麼關係呢？我們再來看看圖。
                    經過觀察，你可以發現，如果在相鄰的兩個線段（或者射線）上任選取兩個點，將這兩點連線，那麼原來的一個區域就會多被分割出來一個。所以每次所有的交點的之間的區域的數量的增加量就為（交點的數量 - 1） ，那麼交點的數量的增加量到底是多少呢？因為是一個折線（在這裡我們可以將其近似考慮成兩條直線），下面大家考慮以下“一條直線與n條直線能有幾個交點?"答案必然是n個 ，所以當一個折線就可以形成2*n（這裡的n表示的是n條直線，所以對於原題的來說一條折線與n條折線的交點數目就為 2*（2*n））個交點，所以第n條折線所有交點間比第n-1的折線的區域數量增加了4*（n-1） - 1 (交點的數量 - 1 )塊，另外需要注意的是，這是一條折線，所以當與其他的線相交過後必然會在其兩端都形成一條射線，這兩條射線也是能夠將區域分割開的，所以分割的增加量除了前面交點形成的增加量意外，還有這兩個射線的增加的  2  塊。
          
             所以就有f(n) = f(n-1) + 4 * (n-1) - 1 + 2;
              化簡的  f(n) = (n-1) + 4 * n - 3;
            

      附上原始碼：

#include<iostream>
#include<algorithm>
using namespace std;
int main()
{
	long long s[10050] = {1,2,7};
	for(int i = 3;i < 10001;i++)
	{
		s[i] = s[i-1] + 4 * i - 3;
	}
	int n;
	cin >> n;
	while(n--)
	{
		int a;
		cin >> a;
		cout << s[a] << endl;
	}
	return 0;
}

另外還有一種就是求其通項公式：

根據直線分平面可知，由交點決定了射線和線段的條數，進而決定了新增的區域數。當n-1條折線時，區域數為f（n-1）。為了使增加的區域最多，則折線的兩邊的線段要和n-1條折線的邊，即2*（n-1）條線段相交。那麼新增的線段數為4*（n-1），射線數為2。但要注意的是，折線本身相鄰的兩線段只能增加一個區域。

       故：f(n)=f(n-1)+4(n-1)+2-1

                      =f(n-1)+4(n-1)+1

                     =f(n-2)+4(n-2)+4(n-1)+2

                     ……

                     =f(1)+4+4*2+……+4(n-1)+(n-1)   

                     =2n^2-n+1

通項公式為：2 * n^2 - n + 1

      附上原始碼：

#include <iostream>
using namespace std;

int main()
{
	int n, m;
	cin >>n;

	while(n--)
	{
		cin >>m;
		cout <<2*m*m - m + 1 <<endl;
	}
	return 0;
}