Hangover

Time Limit: 1000MS	Memory Limit: 10000K
Total Submissions: 89210	Accepted: 43108

Description

How far can you make a stack of cards overhang a table? If you have one card, you can create a maximum overhang of half a card length. (We're assuming that the cards must be perpendicular to the table.) With two cards you can make the top card overhang the bottom one by half a card length, and the bottom one overhang the table by a third of a card length, for a total maximum overhang of 1/2 +

 1/3 = 5/6 card lengths. In general you can make n cards overhang by 1/2 + 1/3 + 1/4 + ... + 1/(n + 1) card lengths, where the top card overhangs the second by 1/2, the second overhangs tha third by 1/3, the third overhangs the fourth by 1/4, etc., and the bottom card overhangs the table by 1/(n + 1). This is illustrated in the figure below.

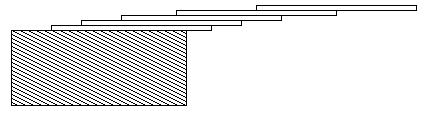
Input

The input consists of one or more test cases, followed by a line containing the number 0.00 that signals the end of the input. Each test case is a single line containing a positive floating-point number c whose value is at least 0.01 and at most 5.20; c will contain exactly three digits.

Output

For each test case, output the minimum number of cards necessary to achieve an overhang of at least c card lengths. Use the exact output format shown in the examples.

Sample Input

1.00
3.71
0.04
5.19
0.00

Sample Output

3 card(s)
61 card(s)
1 card(s)
273 card(s)

題目的意思是： 對於給定的資料，最少需要多少張卡片可以組成這樣的長度 其實就是求這樣的級數和的最小n 注意第二種演算法，通過空間來節省時間

#include <iostream>

using namespace std;

#define MEM_FISRT 1

int main()
{
    double len;
#if MEM_FIRST 
    while(cin >> len && len != 0.00){
        double sum = 0.0;
        double n = 2.0;
        while(1){
            sum += 1.0 / n;
            if (sum >= len) break;
            n += 1.0;
        }   
        cout << (double)n-1 << " card(s)"<< endl;
    }   
#else
    double res[300] = {0.0, 0.5};
    for (int i = 2; i < 300;++i){
        res[i] = res[i-1] + 1.0/(i+1);
    }   
    while(cin >> len && len != 0.00){
        for (int i = 0; i < 300; ++i){
            if (res[i] >= len) {
                cout << i << " card(s)"<< endl;
                break;
            }   
        }   
    }   
#endif


    return 0;
}

參考：