關於傅立葉分析的缺點

使用傅立葉分析，可以對訊號進行頻率分析，但是由於傅立葉分析是對全時域的分析，所以它對於某些特殊訊號頻率在某時段的出現，以及突變訊號，變頻訊號的分析就有不足。

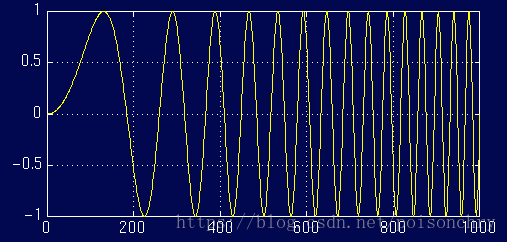
例如，對於如下變頻訊號1：

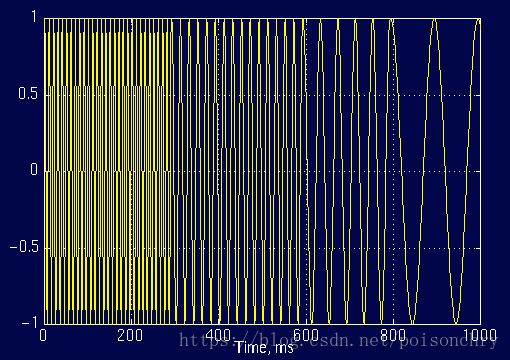
與變頻訊號2：

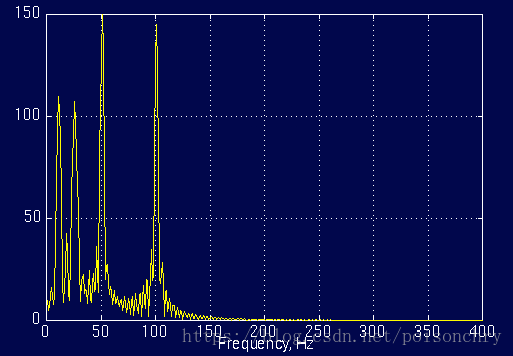
使用傅立葉分析，就會得到一樣的頻率圖

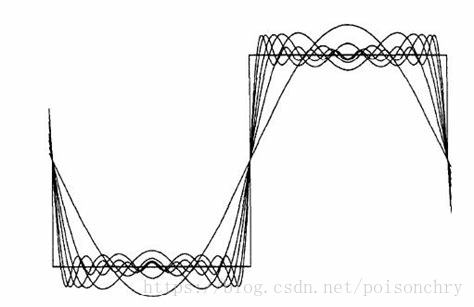
儘管頻率分佈都一樣，但是我們無法從頻率圖上獲得各頻率出現的時間，或許你已經注意到了，與固定頻率的週期訊號相比，這個頻率圖上多出了很多鋸齒狀的頻率分佈，導致這個原因，也是傅立葉分析的另一個缺陷，它對於突變訊號，非連續訊號，需要使用大量高頻訊號去近似擬合，這也意味著傅立葉分析，對於這類訊號，從而導致耗費大量的計算時間（吉布斯效應）。

傅立葉分析的改進方法——短時傅立葉方法（Short Time Fourier Transform）

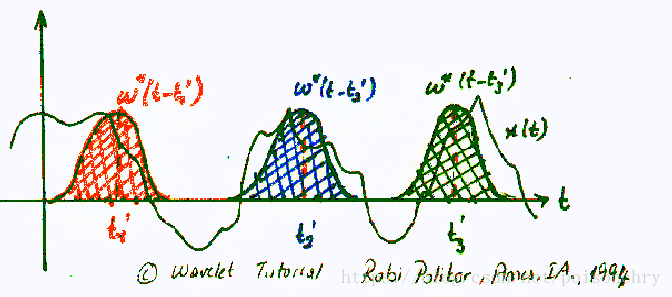
瞭解了傅立葉分析的基本概念，那麼就很容易理解什麼叫短時傅立葉方法，簡寫為STFT。它的核心思想是，將全域性訊號，依照時間間隔T，拆分為獨立的訊號塊，再使用傅立葉分別求解各時間區間內的訊號頻率。

用公式進行表示，就是這樣：

其中，f(t)$f(t)$是原函式，ω(t)$\omega (t)$ 是視窗函式，其中，(t−t∗)$(t-t^{\ast })$表示該函式在時間軸上的位移。如果我們將高斯函式作為平移視窗函式，那麼對於訊號

這個過程，是個類似卷積的過程，如果我們用類似python的偽碼錶示這個過程，需要處理的資料有三個，一個是訊號原始，一個是視窗函式，最後一個是對於一維訊號f(t)$f(t)$，視窗函式ω(t)$\omega (t)$在時間軸上的位移量，T，那麼STFT函式的表示為：

function window_shifting(window_fun, start_time, signal_size): 
    wind = [signal_size]
    set
 
 elements in win to zero
    for i = start_time to signal_size:
        wind[i] = window_fun[i]
    return win

function mat_dot(signal, window):
    if len(signal) is not len(window):
        return false
    for i = 0 to len(signal):
        signal[i] = signal[i] * window[i]
    return signal


function STFT(signal, window, T)
    shifted_window = window_shifting(window, T, len(signal))
    result = mat_dot(signal, shifted_window)

    if result is not false:
        res = fft(result)
        return res

從上示例看，其實window是一個隨時間移動的濾波器，常用的濾波器有理想濾波器，也有高斯濾波器，個人需要針對自己的具體需要選擇合適的濾波器。

參考資料：
[1] “The wavelet tutorial”, Robi Polikar, January 12, 2001.