單目相機成像過程
阿新 • • 發佈:2020-08-03
[toc]
# 單目相機成像過程
## 01 理想情況下相機成像模型
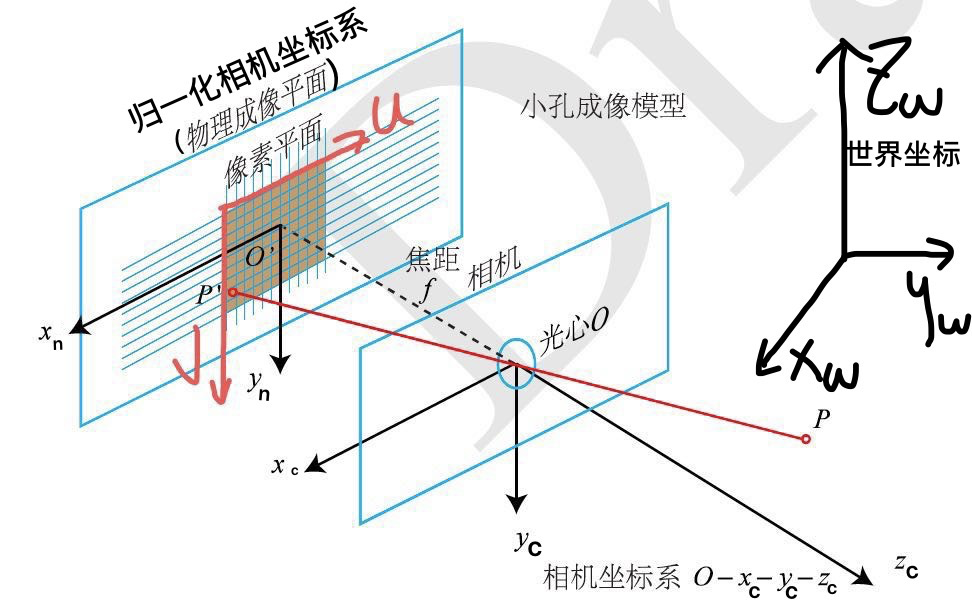
在理想情況下,相機成像模型可以看作是小孔成像模型:
|  |
| :----------------------------------------------------------: |
| 相機成像模型 |
為了便於計算,我們將像平面進行翻轉,它們在數學上是等價的,並且相機硬體會自動幫我們處理,我們假設成像平面翻轉到了相機光心的正前方。相機模型如下,其主要包含4個座標系:
|
|
| :----------------------------------------------------------: |
| 相機成像模型 |
為了便於計算,我們將像平面進行翻轉,它們在數學上是等價的,並且相機硬體會自動幫我們處理,我們假設成像平面翻轉到了相機光心的正前方。相機模型如下,其主要包含4個座標系:
| 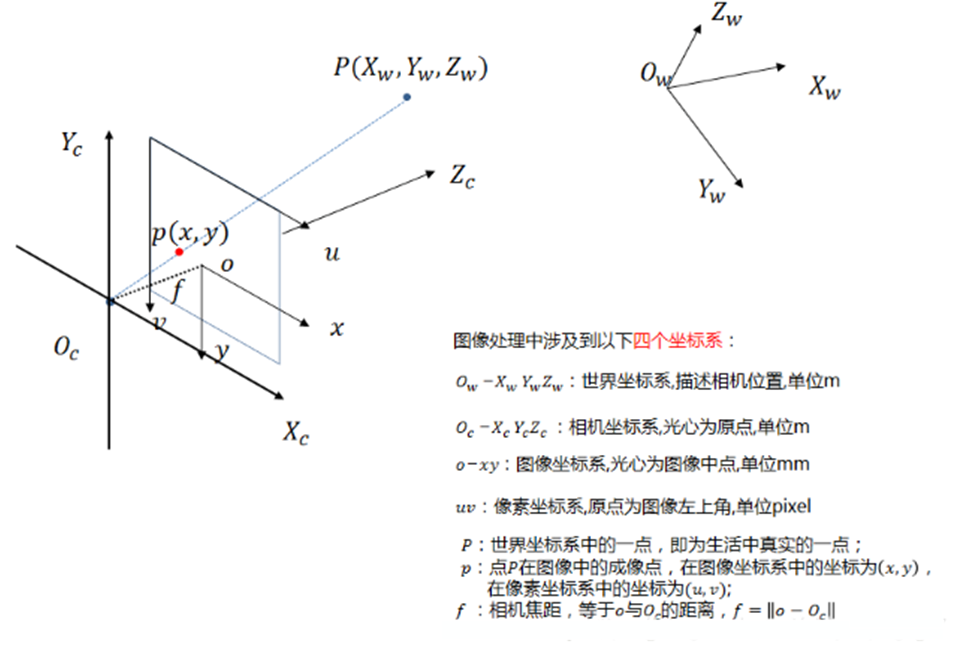 |
| :----------------------------------------------------------: |
| **圖1 相機程式系統中的四大座標系** |
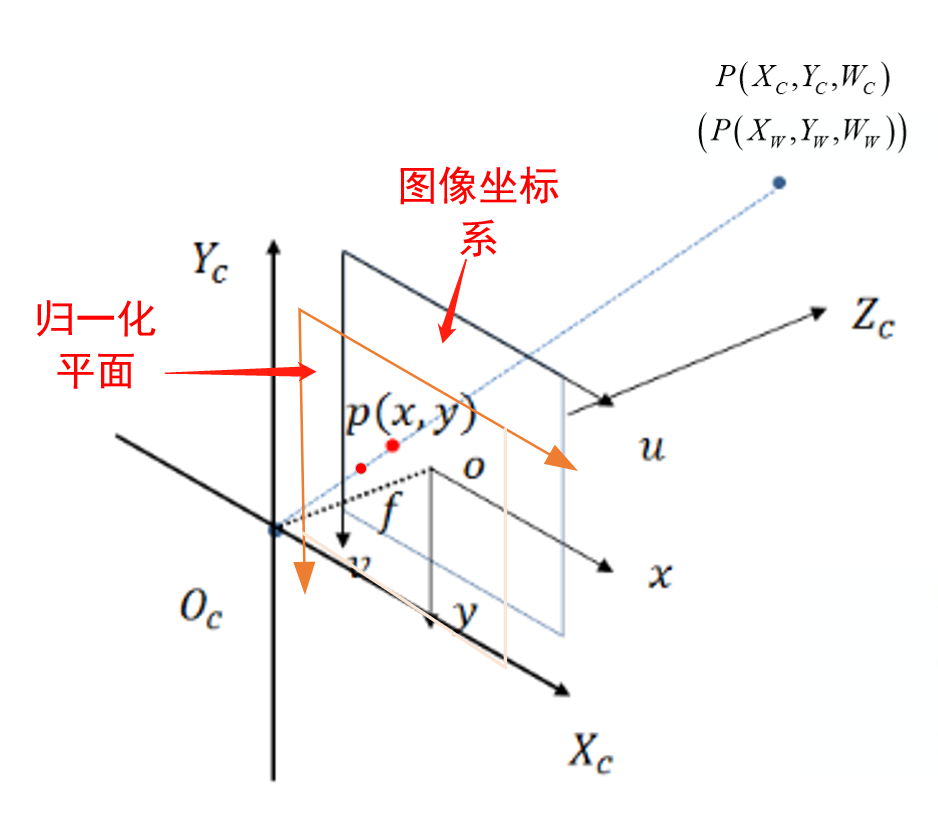
此外,還有一個**歸一化平面**,其實際是影象座標系的等比縮放,也就是當 $f=1$的情況,主要是便於公式推導,它與影象座標系是等比縮放關係,只需要乘以 $f$ 即可完成相互轉換。
|
|
| :----------------------------------------------------------: |
| **圖1 相機程式系統中的四大座標系** |
此外,還有一個**歸一化平面**,其實際是影象座標系的等比縮放,也就是當 $f=1$的情況,主要是便於公式推導,它與影象座標系是等比縮放關係,只需要乘以 $f$ 即可完成相互轉換。
| 
 |
| :----------------------------------------------------------: |
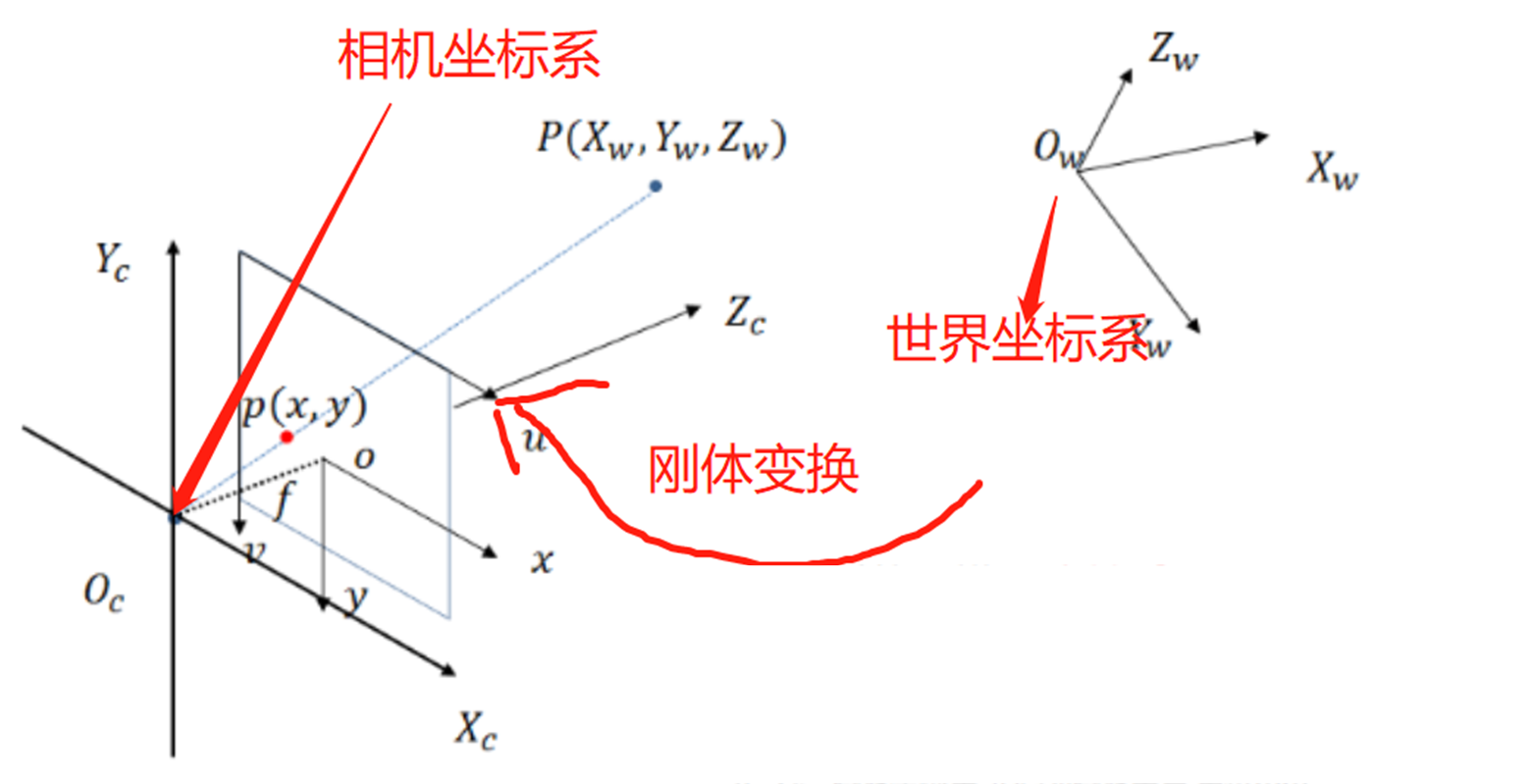
| **圖3 世界座標系 -> 相機座標系(剛體變換)** |
假設該點世界座標系為 $[X_W,Y_W,Z_W]^T$,世界座標系到相機座標系的變換是一個**剛體變換**,那麼同樣的該點,在相機座標系下的座標 $[X_C,Y_C,Z_C]^T$ 如下:
$$
\left[ {\begin{array}{*{20}{c}}
{{X_c}}\\
{{Y_c}}\\
{{Z_c}}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{{r_{11}}}&{{r_{12}}}&{{r_{13}}}\\
{{r_{21}}}&{{r_{22}}}&{{r_{23}}}\\
{{r_{31}}}&{{r_{32}}}&{{r_{33}}}
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
{{X_W}}\\
{{Y_W}}\\
{{Z_W}}
\end{array}} \right] + \left[ {\begin{array}{*{20}{c}}
{{T_x}}\\
{{T_y}}\\
{{T_z}}
\end{array}} \right]
$$
為了將**旋轉矩陣**和**平移矩陣**兩個矩陣形式統一,需要引入齊次座標表示形式:
$$
\underbrace {\left[ {\begin{array}{*{20}{c}}
{{X_C}}\\
{{Y_C}}\\
{{Z_C}}\\
1
\end{array}} \right]}_{相機座標系} = \underbrace {\left[ {\begin{array}{*{20}{c}}
{{R_{3 \times 3}}}&{{T_{3 \times 1}}}\\
0&1
\end{array}} \right]}_{剛體變換}\underbrace {\left[ {\begin{array}{*{20}{c}}
{{X_W}}\\
{{Y_W}}\\
{{Z_W}}\\
1
\end{array}} \right]}_{世界座標系}
$$
### 2)相機座標系 -> 影象座標系
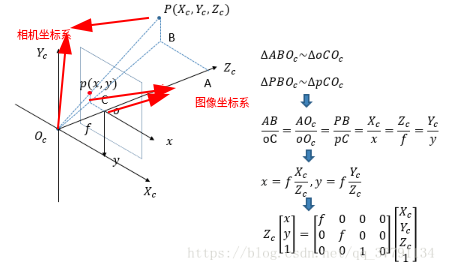
從**相機座標系** $[X_C,Y_C, Z_C,1]^T$ 到 **影象座標系** $[x,y]^T$(成像平面) 的變換是個相似三角形變換,推導如下:
|
|
| :----------------------------------------------------------: |
| **圖3 世界座標系 -> 相機座標系(剛體變換)** |
假設該點世界座標系為 $[X_W,Y_W,Z_W]^T$,世界座標系到相機座標系的變換是一個**剛體變換**,那麼同樣的該點,在相機座標系下的座標 $[X_C,Y_C,Z_C]^T$ 如下:
$$
\left[ {\begin{array}{*{20}{c}}
{{X_c}}\\
{{Y_c}}\\
{{Z_c}}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{{r_{11}}}&{{r_{12}}}&{{r_{13}}}\\
{{r_{21}}}&{{r_{22}}}&{{r_{23}}}\\
{{r_{31}}}&{{r_{32}}}&{{r_{33}}}
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
{{X_W}}\\
{{Y_W}}\\
{{Z_W}}
\end{array}} \right] + \left[ {\begin{array}{*{20}{c}}
{{T_x}}\\
{{T_y}}\\
{{T_z}}
\end{array}} \right]
$$
為了將**旋轉矩陣**和**平移矩陣**兩個矩陣形式統一,需要引入齊次座標表示形式:
$$
\underbrace {\left[ {\begin{array}{*{20}{c}}
{{X_C}}\\
{{Y_C}}\\
{{Z_C}}\\
1
\end{array}} \right]}_{相機座標系} = \underbrace {\left[ {\begin{array}{*{20}{c}}
{{R_{3 \times 3}}}&{{T_{3 \times 1}}}\\
0&1
\end{array}} \right]}_{剛體變換}\underbrace {\left[ {\begin{array}{*{20}{c}}
{{X_W}}\\
{{Y_W}}\\
{{Z_W}}\\
1
\end{array}} \right]}_{世界座標系}
$$
### 2)相機座標系 -> 影象座標系
從**相機座標系** $[X_C,Y_C, Z_C,1]^T$ 到 **影象座標系** $[x,y]^T$(成像平面) 的變換是個相似三角形變換,推導如下:
| 
 1. **世界座標系到相機座標系**:
$$
\underbrace {\left[ {\begin{array}{*{20}{c}}
{{X_C}}\\
{{Y_C}}\\
{{Z_C}}\\
1
\end{array}} \right]}_{相機座標系} = \underbrace {\left[ {\begin{array}{*{20}{c}}
{{R_{3 \times 3}}}&{{T_{3 \times 1}}}\\
0&1
\end{array}} \right]}_{剛體變換}\underbrace {\left[ {\begin{array}{*{20}{c}}
{{X_W}}\\
{{Y_W}}\\
{{Z_W}}\\
1
\end{array}} \right]}_{世界座標系}
$$
2. **相機座標系到影象座標系**:
$$
{Z_c}\underbrace {\left[ {\begin{array}{*{20}{c}}
x\\
y\\
1
\end{array}} \right]}_{\rm{影象座標系}} = \underbrace {\left[ {\begin{array}{*{20}{c}}
f&0&0&0\\
0&f&0&0\\
0&0&1&0
\end{array}} \right]}_{相似三角}\underbrace {\left[ {\begin{array}{*{20}{c}}
{{X_C}}\\
{{Y_C}}\\
{{Z_C}}\\
1
\end{array}} \right]}_{相機座標系}
$$
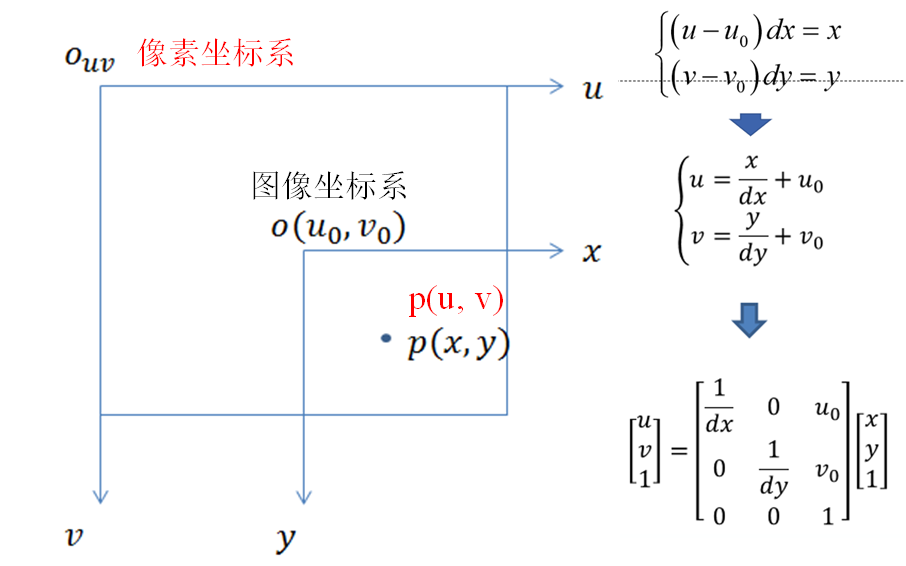
3. **影象座標系到畫素座標系**:
$$
\underbrace {\left[ {\begin{array}{*{20}{c}}
u\\
v\\
1
\end{array}} \right]}_{畫素座標系} = \underbrace {\left[ {\begin{array}{*{20}{c}}
{\frac{1}{{dx}}}&0&{{u_0}}\\
0&{\frac{1}{{dy}}}&{{v_0}}\\
0&0&1
\end{array}} \right]}_{平移+縮放}\underbrace {\left[ {\begin{array}{*{20}{c}}
x\\
y\\
1
\end{array}} \right]}_{影象座標系}
$$
將之前所有的變換合併,可以得到:
$$
{Z_c}\underbrace {\left[ {\begin{array}{*{20}{c}}
u\\
v\\
1
\end{array}} \right]}_{畫素座標系} = \underbrace {\left[ {\begin{array}{*{20}{c}}
{\frac{1}{{dx}}}&0&{{u_0}}\\
0&{\frac{1}{{dy}}}&{{v_0}}\\
0&0&1
\end{array}} \right]}_{03 \ 平移+縮放}\underbrace {\left[ {\begin{array}{*{20}{c}}
f&0&0&0\\
0&f&0&0\\
0&0&1&0
\end{array}} \right]}_{02\ 相似三角形}\underbrace {\left[ {\begin{array}{*{20}{c}}
{{R_{3 \times 3}}}&{{T_{3 \times 1}}}\\
0&1
\end{array}} \right]}_{01 \ 剛體變換}\underbrace {\left[ {\begin{array}{*{20}{c}}
{{X_W}}\\
{{Y_W}}\\
{{Z_W}}\\
1
\end{array}} \right]}_{世界座標系}
$$
將它們相乘後化簡:
$$
{Z_c}\underbrace {\left[ {\begin{array}{*{20}{c}}
u \\
v \\
1
\end{array}} \right]}_{畫素座標系} = \underbrace {\left[ {\begin{array}{*{20}{c}}
{{f_x}}&0&{{u_0}} \\
0&{{f_y}}&{{v_0}} \\
0&0&1
\end{array}} \right]}_{M1:內參}\underbrace {\left[ {\begin{array}{*{20}{c}}
{{R_{3 \times 3}}}&{{T_{3 \times 1}}}
\end{array}} \right]}_{M2:外參}\underbrace {\left[ {\begin{array}{*{20}{c}}
{{X_W}} \\
{{Y_W}} \\
{{Z_W}} \\
1
\end{array}} \right]}_{世界座標系}
$$
以上是理想情況下世界座標系到畫素座標系的轉換,而由於相機制造工藝的原因,其成像過程中難免存在著畸變,在後續構建精確的三維重建演算法前,我們要對相機的畸變進行矯正,以提高演算法重建的精度,這一步驟也稱為**相機標定**。
## 02 考慮畸變情況下相機成像模型
相機畸變主要有兩種型別:**徑向畸變** 和 **切向畸變**,我們分別介紹這兩種情況。
### 1)徑向畸變
> **原因**:在相機制造過程中,很難保證鏡頭的厚度完全均勻,由於製造工藝的原因,通常為這種情況為中間厚、邊緣薄,因而光線在遠離透鏡中心的地方,會發生更大程度的扭曲,這種現象在魚眼相機(桶形畸變)中尤為明顯。
徑向畸變主要有兩種型別:**枕型畸變**和**桶型畸變**,示意圖如下:
|
1. **世界座標系到相機座標系**:
$$
\underbrace {\left[ {\begin{array}{*{20}{c}}
{{X_C}}\\
{{Y_C}}\\
{{Z_C}}\\
1
\end{array}} \right]}_{相機座標系} = \underbrace {\left[ {\begin{array}{*{20}{c}}
{{R_{3 \times 3}}}&{{T_{3 \times 1}}}\\
0&1
\end{array}} \right]}_{剛體變換}\underbrace {\left[ {\begin{array}{*{20}{c}}
{{X_W}}\\
{{Y_W}}\\
{{Z_W}}\\
1
\end{array}} \right]}_{世界座標系}
$$
2. **相機座標系到影象座標系**:
$$
{Z_c}\underbrace {\left[ {\begin{array}{*{20}{c}}
x\\
y\\
1
\end{array}} \right]}_{\rm{影象座標系}} = \underbrace {\left[ {\begin{array}{*{20}{c}}
f&0&0&0\\
0&f&0&0\\
0&0&1&0
\end{array}} \right]}_{相似三角}\underbrace {\left[ {\begin{array}{*{20}{c}}
{{X_C}}\\
{{Y_C}}\\
{{Z_C}}\\
1
\end{array}} \right]}_{相機座標系}
$$
3. **影象座標系到畫素座標系**:
$$
\underbrace {\left[ {\begin{array}{*{20}{c}}
u\\
v\\
1
\end{array}} \right]}_{畫素座標系} = \underbrace {\left[ {\begin{array}{*{20}{c}}
{\frac{1}{{dx}}}&0&{{u_0}}\\
0&{\frac{1}{{dy}}}&{{v_0}}\\
0&0&1
\end{array}} \right]}_{平移+縮放}\underbrace {\left[ {\begin{array}{*{20}{c}}
x\\
y\\
1
\end{array}} \right]}_{影象座標系}
$$
將之前所有的變換合併,可以得到:
$$
{Z_c}\underbrace {\left[ {\begin{array}{*{20}{c}}
u\\
v\\
1
\end{array}} \right]}_{畫素座標系} = \underbrace {\left[ {\begin{array}{*{20}{c}}
{\frac{1}{{dx}}}&0&{{u_0}}\\
0&{\frac{1}{{dy}}}&{{v_0}}\\
0&0&1
\end{array}} \right]}_{03 \ 平移+縮放}\underbrace {\left[ {\begin{array}{*{20}{c}}
f&0&0&0\\
0&f&0&0\\
0&0&1&0
\end{array}} \right]}_{02\ 相似三角形}\underbrace {\left[ {\begin{array}{*{20}{c}}
{{R_{3 \times 3}}}&{{T_{3 \times 1}}}\\
0&1
\end{array}} \right]}_{01 \ 剛體變換}\underbrace {\left[ {\begin{array}{*{20}{c}}
{{X_W}}\\
{{Y_W}}\\
{{Z_W}}\\
1
\end{array}} \right]}_{世界座標系}
$$
將它們相乘後化簡:
$$
{Z_c}\underbrace {\left[ {\begin{array}{*{20}{c}}
u \\
v \\
1
\end{array}} \right]}_{畫素座標系} = \underbrace {\left[ {\begin{array}{*{20}{c}}
{{f_x}}&0&{{u_0}} \\
0&{{f_y}}&{{v_0}} \\
0&0&1
\end{array}} \right]}_{M1:內參}\underbrace {\left[ {\begin{array}{*{20}{c}}
{{R_{3 \times 3}}}&{{T_{3 \times 1}}}
\end{array}} \right]}_{M2:外參}\underbrace {\left[ {\begin{array}{*{20}{c}}
{{X_W}} \\
{{Y_W}} \\
{{Z_W}} \\
1
\end{array}} \right]}_{世界座標系}
$$
以上是理想情況下世界座標系到畫素座標系的轉換,而由於相機制造工藝的原因,其成像過程中難免存在著畸變,在後續構建精確的三維重建演算法前,我們要對相機的畸變進行矯正,以提高演算法重建的精度,這一步驟也稱為**相機標定**。
## 02 考慮畸變情況下相機成像模型
相機畸變主要有兩種型別:**徑向畸變** 和 **切向畸變**,我們分別介紹這兩種情況。
### 1)徑向畸變
> **原因**:在相機制造過程中,很難保證鏡頭的厚度完全均勻,由於製造工藝的原因,通常為這種情況為中間厚、邊緣薄,因而光線在遠離透鏡中心的地方,會發生更大程度的扭曲,這種現象在魚眼相機(桶形畸變)中尤為明顯。
徑向畸變主要有兩種型別:**枕型畸變**和**桶型畸變**,示意圖如下:
|  |
|  |
| :----------------------------------------------------------: | :----------------------------------------------------------: |
|
|
| :----------------------------------------------------------: | :----------------------------------------------------------: |
|  |
|  |
| **桶型畸變** | **枕形畸變** |
它們可以由 $k_1,k_2$ 構成的下列數學公式描述:
$$
\left[ {\begin{array}{*{20}{c}}
{x'}\\
{y'}
\end{array}} \right] = (1 + {k_1}{r^2} + {k_2}{r^4} + {k_3}{r^6})\left[ {\begin{array}{*{20}{c}}
x\\
y
\end{array}} \right]
$$
其中:
- $r$ 為曲率半徑,有:$r^2 =x^2 + y^2$;
- $k_1,k_2,k_3$ 為徑向畸變係數;
- $x, y$ 為發生畸變后角點的座標,也就是我們實際看到的;
- $x',y'$ 為畸變矯正,也就是去除畸變後的正確座標;
> 注:這裡無論是 $x, y,x',y'$,其均為歸一化平面上角點的座標。
通常:我們只用 $k_1,k_2$ 來矯正相機,對於畸變較小的影象中心區域,主要是 $k_1$ 在起作用,對於畸變較大的影象邊緣區域,主要是 $k_2$ 在起作用,而對於魚眼相機這類廣角相機,我們才會用 $k_3$。需要注意的是,這裡並不是用的係數越多,整個矯正結果越精確,我們應該考慮相機的實際情況。
### 2)切向畸變
> **原因**:切向畸變產生的原因在於相機在製造過程中,成像平面與透鏡平面不平行,產生了透視變換。
|
| **桶型畸變** | **枕形畸變** |
它們可以由 $k_1,k_2$ 構成的下列數學公式描述:
$$
\left[ {\begin{array}{*{20}{c}}
{x'}\\
{y'}
\end{array}} \right] = (1 + {k_1}{r^2} + {k_2}{r^4} + {k_3}{r^6})\left[ {\begin{array}{*{20}{c}}
x\\
y
\end{array}} \right]
$$
其中:
- $r$ 為曲率半徑,有:$r^2 =x^2 + y^2$;
- $k_1,k_2,k_3$ 為徑向畸變係數;
- $x, y$ 為發生畸變后角點的座標,也就是我們實際看到的;
- $x',y'$ 為畸變矯正,也就是去除畸變後的正確座標;
> 注:這裡無論是 $x, y,x',y'$,其均為歸一化平面上角點的座標。
通常:我們只用 $k_1,k_2$ 來矯正相機,對於畸變較小的影象中心區域,主要是 $k_1$ 在起作用,對於畸變較大的影象邊緣區域,主要是 $k_2$ 在起作用,而對於魚眼相機這類廣角相機,我們才會用 $k_3$。需要注意的是,這裡並不是用的係數越多,整個矯正結果越精確,我們應該考慮相機的實際情況。
### 2)切向畸變
> **原因**:切向畸變產生的原因在於相機在製造過程中,成像平面與透鏡平面不平行,產生了透視變換。
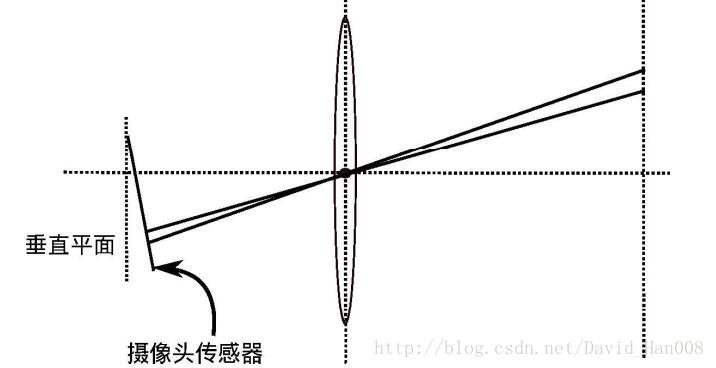
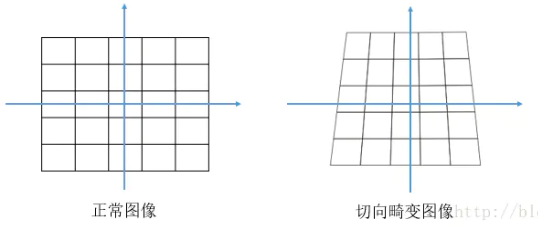 這種畸變可以由以下公式描述,它也與距離影象中心的距離半徑有關:
$$
\left[ {\begin{array}{*{20}{c}}
x'\\
y'
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{2{p_1}xy + {p_2}\left( {{r^2} + 2{x^2}} \right)}\\
{2{p_2}xy + {p_1}\left( {{r^2} + 2{y^2}} \right)}
\end{array}} \right]
$$
其中:$p_1,p_2$ 稱為切向畸變矯正係數,其它的含義與徑向畸變中公式相同。
### 3)合併考慮畸變
> 原因:其實也很簡單,兩種畸變是同時發生在成像過程中的,發生的原因也是相互獨立的,而且也都是關於距離的表示式,你似乎也找不到更好的方式來綜合考慮這兩種誤差,實踐證明,這種合併考慮畸變的情況效果還不錯。
將徑向畸變和切向畸變合併,只需要將兩個畸變矯正直接加起來即可,公式如下:
$$
\left[ {\begin{array}{*{20}{c}}
{x'}\\
{y'}
\end{array}} \right] = \underbrace {\left( {1 + {k_1}{r^2} + {k_2}{r^4} + {k_3}{r^6}} \right)\left[ {\begin{array}{*{20}{c}}
x\\
y
\end{array}} \right]}_{徑向畸變} + \underbrace {\left[ {\begin{array}{*{20}{c}}
{2{p_1}xy + {p_2}\left( {{r^2} + 2{x^2}} \right)}\\
{2{p_2}xy + p1\left( {{r^2} + 2{y^2}} \right)}
\end{array}} \right]}_{切向畸變}
$$
其中:
- $k_1,k_2,k_3$ 為徑向畸變係數;
- $p_1,p_2$ 為切向畸變係數;
不過在此之前,我們特別注意一點,相機畸變現象發生的位置:
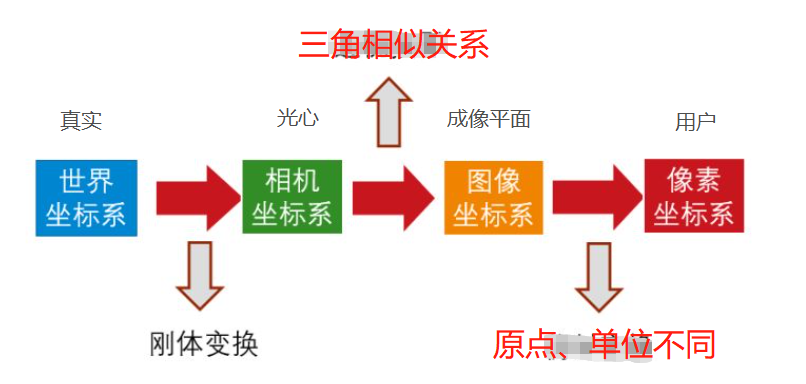
- **世界座標系 -> 相機座標系**,剛體變換,不存在畸變現象;
- **相機座標系 -> 影象座標系**,也就是成像過程,理想情況下是相似三角形,但實際由於相機制造、裝配的原因,成像過程存在畸變現象;
- **影象座標系 -> 畫素座標系**,座標原點、單位不同,僅僅平移與縮放,不存在畸變現象;
## 03 成像過程總結
現在,我們將這些公式進行整理,假設:
- 某點世界座標系為$P(X_W,Y_W,Z_W)$;
- 對應的實際得到的畫素座標系為 $P(u,v)$(未矯正的);
- 正確的畫素座標為 $P(u',v')$;
- 假設我們已知畸變係數 $k_1,k_2,k_3,p_1,p_2$;
那麼從世界座標系 $P(X_W,Y_W,Z_W)$ 到正確的畫素座標系 $P(u',v')$ 的推導如下,對於畫素座標系下某點 $P(u,v)$,有:
1. **畫素座標系 -> 歸一化座標系**
這個變換僅僅是平移與縮放,不存在畸變,因而只需要一個逆變換,歸一化座標 $P=(x,y)^T$ 推導如下:
$$
\begin{array}{c}
\underbrace {\left[ {\begin{array}{*{20}{c}}
u\\
v\\
1
\end{array}} \right]}_{畫素座標} = \underbrace {\left[ {\begin{array}{*{20}{c}}
{\frac{1}{{dx}}}&0&{{u_0}}\\
0&{\frac{1}{{dy}}}&{{v_0}}\\
0&0&1
\end{array}} \right]}_{平移+縮放}\underbrace {\left( {\underbrace {\left[ {\begin{array}{*{20}{c}}
x\\
y\\
{1/f}
\end{array}} \right]}_{歸一化座標} \times f} \right)}_{影象座標}
\\
\Downarrow
\\
\underbrace {\left[ {\begin{array}{*{20}{c}}
x\\
y\\
{1/f}
\end{array}} \right]}_{歸一化座標} = \underbrace {\left( {{{\left[ {\begin{array}{*{20}{c}}
{\frac{1}{{dx}}}&0&{{u_0}}\\
0&{\frac{1}{{dy}}}&{{v_0}}\\
0&0&1
\end{array}} \right]}^{ - 1}}\underbrace {\left[ {\begin{array}{*{20}{c}}
u\\
v\\
1
\end{array}} \right]}_{畫素座標}} \right)}_{影象座標}/f
\end{array}
$$
2. **歸一化座標系(帶畸變的) -> 歸一化座標系(畸變矯正後)**
在前一成像過程,也就是相機座標系到歸一化平面透射中,相機發生了畸變,因而我們需要將實際的歸一化座標 $P=(x,y)^T$ 糾正到理想的無畸變歸一化座標 $P=(x',y')^T$:
$$
\left[ {\begin{array}{*{20}{c}}
{x'}\\
{y'}\\
{1/f}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{\left( {1 + {k_1}{r^2} + {k_2}{r^4} + {k_3}{r^6}} \right)x + 2{p_1}xy + {p_2}\left( {{r^2} + 2{x^2}} \right)}\\
{\left( {1 + {k_1}{r^2} + {k_2}{r^4} + {k_3}{r^6}} \right)y + 2{p_2}xy + {p_1}\left( {{r^2} + 2{y^2}} \right)}\\
{1/f}
\end{array}} \right]
$$
3. **歸一化座標系(理想)-> 相機座標系**
理想的無畸變歸一化座標 $P=(x',y')$ 到相機座標系,它們是相似三角形關係:
$$
{Z_c}\underbrace {\left( {\underbrace {\left[ {\begin{array}{*{20}{c}}
{x'}\\
{y'}\\
1/f
\end{array}} \right]}_{歸一化座標系(準確)} \cdot f} \right)}_{影象座標}
= \underbrace {\left[ {\begin{array}{*{20}{c}}
f&0&0&0\\
0&f&0&0\\
0&0&1&0
\end{array}} \right]}_{相似三角形}\underbrace {\left[ {\begin{array}{*{20}{c}}
{{X_C}}\\
{{Y_C}}\\
{{Z_C}}\\
1
\end{array}} \right]}_{相機座標} \\
\Downarrow
\\
\left[ {\begin{array}{*{20}{c}}
{{X_c}}\\
{{Y_c}}\\
{{Z_c}}\\
1
\end{array}} \right] = f \cdot {Z_c} \cdot {\left[ {\begin{array}{*{20}{c}}
f&0&0&0\\
0&f&0&0\\
0&0&1&0
\end{array}} \right]^{ - 1}}\left[ {\begin{array}{*{20}{c}}
{x'}\\
{y'}\\
{1/f}
\end{array}} \right]
$$
注:這裡 $3 \times 4$ 矩陣的逆是偽逆。
4. **相機座標系 -> 世界座標系**
相機座標系到世界座標系,僅僅是之前剛體變換的反變換:
$$
\underbrace {\left[ {\begin{array}{*{20}{c}}
{{X_C}}\\
{{Y_C}}\\
{{Z_C}}\\
1
\end{array}} \right]}_{相機座標系} = \underbrace {\left[ {\begin{array}{*{20}{c}}
{{R_{3 \times 3}}}&{{T_{3 \times 1}}}\\
0&1
\end{array}} \right]}_{剛體變換}\underbrace {\left[ {\begin{array}{*{20}{c}}
{{X_W}}\\
{{Y_W}}\\
{{Z_W}}\\
1
\end{array}} \right]}_{世界座標系}
\\
\Downarrow
\\
\left[ {\begin{array}{*{20}{c}}
{{X_W}}\\
{{Y_W}}\\
{{Z_W}}\\
1
\end{array}} \right] = {\left[ {\begin{array}{*{20}{c}}
{{R_{3 \times 3}}}&{{T_{3 \times 1}}}\\
0&1
\end{array}} \right]^{ - 1}}\left[ {\begin{array}{*{20}{c}}
{{X_C}}\\
{{Y_c}}\\
{{Z_c}}\\
1
\end{array}} \right]
$$
所以,我們只需要將上述的四個公式合併起來即可,畫素座標系$P=(u,v)$轉換到世界座標系 $P=(X_W,Y_W,Z_W)$。
## 04 思考問題
現在的問題是,我們如何求得這些畸變係數 $k_1,k_2,k_3,p_1,p_2$?得到這些係數之後,我們就能建立畫素座標系與世界座標系的對映。這個問題可以由**張正友標定法**來實現。
> 對於張正友標定法的原理,略微有些複雜,在下一節推送中,我們從它的實現開始講起,然後如果你們有興趣,可以看我們的拓展閱讀《張正友標定法數學基礎及原理推導》。
先回過頭來看前面的式子,我們可以看到,即使考慮了畸變,從畫素座標系到世界座標系的轉換,其實還是一些乘法運算,但是這裡有兩個問題需要大家思考:
### 1)問題一
對於考慮了畸變的相機模型,世界座標系與畫素座標系之間的轉換公式,其實是存在一個問題的:不能寫成完全矩陣$x,y$ 的乘法形式。因為相機模型的切向畸變部分包含非線性項 $xy,x^2,y^2$:
$$
\left[ {\begin{array}{*{20}{c}}
{x'}\\
{y'}
\end{array}} \right] = \underbrace {\left( {1 + {k_1}{r^2} + {k_2}{r^4} + {k_3}{r^6}} \right)\left[ {\begin{array}{*{20}{c}}
x\\
y
\end{array}} \right]}_{徑向畸變} + \underbrace {\left[ {\begin{array}{*{20}{c}}
{2{p_1}xy + {p_2}\left( {{r^2} + 2{x^2}} \right)}\\
{2{p_2}xy + p1\left( {{r^2} + 2{y^2}} \right)}
\end{array}} \right]}_{切向畸變}
$$
> 有人說,這樣似乎也沒什麼問題嘛,無非是計算速度慢一點而已,但事情不是這樣的,矩陣方程裡存在著非線性項,而且還有一個加法,我們那些關於方程組解、求特徵值、正定、半正定、正交這些理論武器,全部都失去作用了。
事實上,一些質量較好的工業相機,切向畸變都是很小的(話說,相機都不準,你拿它做什麼精確的三維重建…),張正友標定法在初始的時候即假設相機不存在徑向畸變(之後會求),也就是 $p_1,p_2$ 都等於零,另外同樣$k3=0$。這樣的好處在於,考慮畸變的相機模型,在初期跟理想模型的差別在於乘以一個常數項,整個式子就可以寫為一個單應性矩陣的形式,方便我們對方程組進行優化:
$$
s\tilde m = A\left[ {\begin{array}{*{20}{c}}
{{R_{3 \times 3}}}&{{T_{3 \times 1}}}
\end{array}} \right]\tilde M
$$
其中:
- $s$ 稱為尺度因子;
- $\tilde m $ 為畫素座標系,$\tilde M $ 為世界座標系;
- $A$ 為單應性矩陣;
- $[R_{3 \times 3} \ T_{3\times1}]$ 是外參矩陣;
### 2)問題二
還有個問題,假設我們得到了這些畸變係數,能否由畫素座標系推導到世界座標系?事實上是不能的,比如下面這種圖:
|
這種畸變可以由以下公式描述,它也與距離影象中心的距離半徑有關:
$$
\left[ {\begin{array}{*{20}{c}}
x'\\
y'
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{2{p_1}xy + {p_2}\left( {{r^2} + 2{x^2}} \right)}\\
{2{p_2}xy + {p_1}\left( {{r^2} + 2{y^2}} \right)}
\end{array}} \right]
$$
其中:$p_1,p_2$ 稱為切向畸變矯正係數,其它的含義與徑向畸變中公式相同。
### 3)合併考慮畸變
> 原因:其實也很簡單,兩種畸變是同時發生在成像過程中的,發生的原因也是相互獨立的,而且也都是關於距離的表示式,你似乎也找不到更好的方式來綜合考慮這兩種誤差,實踐證明,這種合併考慮畸變的情況效果還不錯。
將徑向畸變和切向畸變合併,只需要將兩個畸變矯正直接加起來即可,公式如下:
$$
\left[ {\begin{array}{*{20}{c}}
{x'}\\
{y'}
\end{array}} \right] = \underbrace {\left( {1 + {k_1}{r^2} + {k_2}{r^4} + {k_3}{r^6}} \right)\left[ {\begin{array}{*{20}{c}}
x\\
y
\end{array}} \right]}_{徑向畸變} + \underbrace {\left[ {\begin{array}{*{20}{c}}
{2{p_1}xy + {p_2}\left( {{r^2} + 2{x^2}} \right)}\\
{2{p_2}xy + p1\left( {{r^2} + 2{y^2}} \right)}
\end{array}} \right]}_{切向畸變}
$$
其中:
- $k_1,k_2,k_3$ 為徑向畸變係數;
- $p_1,p_2$ 為切向畸變係數;
不過在此之前,我們特別注意一點,相機畸變現象發生的位置:
- **世界座標系 -> 相機座標系**,剛體變換,不存在畸變現象;
- **相機座標系 -> 影象座標系**,也就是成像過程,理想情況下是相似三角形,但實際由於相機制造、裝配的原因,成像過程存在畸變現象;
- **影象座標系 -> 畫素座標系**,座標原點、單位不同,僅僅平移與縮放,不存在畸變現象;
## 03 成像過程總結
現在,我們將這些公式進行整理,假設:
- 某點世界座標系為$P(X_W,Y_W,Z_W)$;
- 對應的實際得到的畫素座標系為 $P(u,v)$(未矯正的);
- 正確的畫素座標為 $P(u',v')$;
- 假設我們已知畸變係數 $k_1,k_2,k_3,p_1,p_2$;
那麼從世界座標系 $P(X_W,Y_W,Z_W)$ 到正確的畫素座標系 $P(u',v')$ 的推導如下,對於畫素座標系下某點 $P(u,v)$,有:
1. **畫素座標系 -> 歸一化座標系**
這個變換僅僅是平移與縮放,不存在畸變,因而只需要一個逆變換,歸一化座標 $P=(x,y)^T$ 推導如下:
$$
\begin{array}{c}
\underbrace {\left[ {\begin{array}{*{20}{c}}
u\\
v\\
1
\end{array}} \right]}_{畫素座標} = \underbrace {\left[ {\begin{array}{*{20}{c}}
{\frac{1}{{dx}}}&0&{{u_0}}\\
0&{\frac{1}{{dy}}}&{{v_0}}\\
0&0&1
\end{array}} \right]}_{平移+縮放}\underbrace {\left( {\underbrace {\left[ {\begin{array}{*{20}{c}}
x\\
y\\
{1/f}
\end{array}} \right]}_{歸一化座標} \times f} \right)}_{影象座標}
\\
\Downarrow
\\
\underbrace {\left[ {\begin{array}{*{20}{c}}
x\\
y\\
{1/f}
\end{array}} \right]}_{歸一化座標} = \underbrace {\left( {{{\left[ {\begin{array}{*{20}{c}}
{\frac{1}{{dx}}}&0&{{u_0}}\\
0&{\frac{1}{{dy}}}&{{v_0}}\\
0&0&1
\end{array}} \right]}^{ - 1}}\underbrace {\left[ {\begin{array}{*{20}{c}}
u\\
v\\
1
\end{array}} \right]}_{畫素座標}} \right)}_{影象座標}/f
\end{array}
$$
2. **歸一化座標系(帶畸變的) -> 歸一化座標系(畸變矯正後)**
在前一成像過程,也就是相機座標系到歸一化平面透射中,相機發生了畸變,因而我們需要將實際的歸一化座標 $P=(x,y)^T$ 糾正到理想的無畸變歸一化座標 $P=(x',y')^T$:
$$
\left[ {\begin{array}{*{20}{c}}
{x'}\\
{y'}\\
{1/f}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{\left( {1 + {k_1}{r^2} + {k_2}{r^4} + {k_3}{r^6}} \right)x + 2{p_1}xy + {p_2}\left( {{r^2} + 2{x^2}} \right)}\\
{\left( {1 + {k_1}{r^2} + {k_2}{r^4} + {k_3}{r^6}} \right)y + 2{p_2}xy + {p_1}\left( {{r^2} + 2{y^2}} \right)}\\
{1/f}
\end{array}} \right]
$$
3. **歸一化座標系(理想)-> 相機座標系**
理想的無畸變歸一化座標 $P=(x',y')$ 到相機座標系,它們是相似三角形關係:
$$
{Z_c}\underbrace {\left( {\underbrace {\left[ {\begin{array}{*{20}{c}}
{x'}\\
{y'}\\
1/f
\end{array}} \right]}_{歸一化座標系(準確)} \cdot f} \right)}_{影象座標}
= \underbrace {\left[ {\begin{array}{*{20}{c}}
f&0&0&0\\
0&f&0&0\\
0&0&1&0
\end{array}} \right]}_{相似三角形}\underbrace {\left[ {\begin{array}{*{20}{c}}
{{X_C}}\\
{{Y_C}}\\
{{Z_C}}\\
1
\end{array}} \right]}_{相機座標} \\
\Downarrow
\\
\left[ {\begin{array}{*{20}{c}}
{{X_c}}\\
{{Y_c}}\\
{{Z_c}}\\
1
\end{array}} \right] = f \cdot {Z_c} \cdot {\left[ {\begin{array}{*{20}{c}}
f&0&0&0\\
0&f&0&0\\
0&0&1&0
\end{array}} \right]^{ - 1}}\left[ {\begin{array}{*{20}{c}}
{x'}\\
{y'}\\
{1/f}
\end{array}} \right]
$$
注:這裡 $3 \times 4$ 矩陣的逆是偽逆。
4. **相機座標系 -> 世界座標系**
相機座標系到世界座標系,僅僅是之前剛體變換的反變換:
$$
\underbrace {\left[ {\begin{array}{*{20}{c}}
{{X_C}}\\
{{Y_C}}\\
{{Z_C}}\\
1
\end{array}} \right]}_{相機座標系} = \underbrace {\left[ {\begin{array}{*{20}{c}}
{{R_{3 \times 3}}}&{{T_{3 \times 1}}}\\
0&1
\end{array}} \right]}_{剛體變換}\underbrace {\left[ {\begin{array}{*{20}{c}}
{{X_W}}\\
{{Y_W}}\\
{{Z_W}}\\
1
\end{array}} \right]}_{世界座標系}
\\
\Downarrow
\\
\left[ {\begin{array}{*{20}{c}}
{{X_W}}\\
{{Y_W}}\\
{{Z_W}}\\
1
\end{array}} \right] = {\left[ {\begin{array}{*{20}{c}}
{{R_{3 \times 3}}}&{{T_{3 \times 1}}}\\
0&1
\end{array}} \right]^{ - 1}}\left[ {\begin{array}{*{20}{c}}
{{X_C}}\\
{{Y_c}}\\
{{Z_c}}\\
1
\end{array}} \right]
$$
所以,我們只需要將上述的四個公式合併起來即可,畫素座標系$P=(u,v)$轉換到世界座標系 $P=(X_W,Y_W,Z_W)$。
## 04 思考問題
現在的問題是,我們如何求得這些畸變係數 $k_1,k_2,k_3,p_1,p_2$?得到這些係數之後,我們就能建立畫素座標系與世界座標系的對映。這個問題可以由**張正友標定法**來實現。
> 對於張正友標定法的原理,略微有些複雜,在下一節推送中,我們從它的實現開始講起,然後如果你們有興趣,可以看我們的拓展閱讀《張正友標定法數學基礎及原理推導》。
先回過頭來看前面的式子,我們可以看到,即使考慮了畸變,從畫素座標系到世界座標系的轉換,其實還是一些乘法運算,但是這裡有兩個問題需要大家思考:
### 1)問題一
對於考慮了畸變的相機模型,世界座標系與畫素座標系之間的轉換公式,其實是存在一個問題的:不能寫成完全矩陣$x,y$ 的乘法形式。因為相機模型的切向畸變部分包含非線性項 $xy,x^2,y^2$:
$$
\left[ {\begin{array}{*{20}{c}}
{x'}\\
{y'}
\end{array}} \right] = \underbrace {\left( {1 + {k_1}{r^2} + {k_2}{r^4} + {k_3}{r^6}} \right)\left[ {\begin{array}{*{20}{c}}
x\\
y
\end{array}} \right]}_{徑向畸變} + \underbrace {\left[ {\begin{array}{*{20}{c}}
{2{p_1}xy + {p_2}\left( {{r^2} + 2{x^2}} \right)}\\
{2{p_2}xy + p1\left( {{r^2} + 2{y^2}} \right)}
\end{array}} \right]}_{切向畸變}
$$
> 有人說,這樣似乎也沒什麼問題嘛,無非是計算速度慢一點而已,但事情不是這樣的,矩陣方程裡存在著非線性項,而且還有一個加法,我們那些關於方程組解、求特徵值、正定、半正定、正交這些理論武器,全部都失去作用了。
事實上,一些質量較好的工業相機,切向畸變都是很小的(話說,相機都不準,你拿它做什麼精確的三維重建…),張正友標定法在初始的時候即假設相機不存在徑向畸變(之後會求),也就是 $p_1,p_2$ 都等於零,另外同樣$k3=0$。這樣的好處在於,考慮畸變的相機模型,在初期跟理想模型的差別在於乘以一個常數項,整個式子就可以寫為一個單應性矩陣的形式,方便我們對方程組進行優化:
$$
s\tilde m = A\left[ {\begin{array}{*{20}{c}}
{{R_{3 \times 3}}}&{{T_{3 \times 1}}}
\end{array}} \right]\tilde M
$$
其中:
- $s$ 稱為尺度因子;
- $\tilde m $ 為畫素座標系,$\tilde M $ 為世界座標系;
- $A$ 為單應性矩陣;
- $[R_{3 \times 3} \ T_{3\times1}]$ 是外參矩陣;
### 2)問題二
還有個問題,假設我們得到了這些畸變係數,能否由畫素座標系推導到世界座標系?事實上是不能的,比如下面這種圖:
|  |
|  |
| :----------------------------------------------------------: | :----------------------------------------------------------: |
| 圖a 單目相機失真 | 圖2 單目相機模型 |
光心 $O_c$ 與$P(X_C,Y_C,Z_C)$ 的整條連線上的三維點,在成像平面的像點均在點 $p(x,y)$ 上。所以在單目相機的標定方法中,甚至不需要知道棋盤格的實際大小也能完成相機的
|
| :----------------------------------------------------------: | :----------------------------------------------------------: |
| 圖a 單目相機失真 | 圖2 單目相機模型 |
光心 $O_c$ 與$P(X_C,Y_C,Z_C)$ 的整條連線上的三維點,在成像平面的像點均在點 $p(x,y)$ 上。所以在單目相機的標定方法中,甚至不需要知道棋盤格的實際大小也能完成相機的
 |
| :----------------------------------------------------------: |
| **圖1 相機程式系統中的四大座標系** |
此外,還有一個**歸一化平面**,其實際是影象座標系的等比縮放,也就是當 $f=1$的情況,主要是便於公式推導,它與影象座標系是等比縮放關係,只需要乘以 $f$ 即可完成相互轉換。
|
|
| :----------------------------------------------------------: |
| **圖1 相機程式系統中的四大座標系** |
此外,還有一個**歸一化平面**,其實際是影象座標系的等比縮放,也就是當 $f=1$的情況,主要是便於公式推導,它與影象座標系是等比縮放關係,只需要乘以 $f$ 即可完成相互轉換。
| 
 |
| :----------------------------------------------------------: |
| **圖3 世界座標系 -> 相機座標系(剛體變換)** |
假設該點世界座標系為 $[X_W,Y_W,Z_W]^T$,世界座標系到相機座標系的變換是一個**剛體變換**,那麼同樣的該點,在相機座標系下的座標 $[X_C,Y_C,Z_C]^T$ 如下:
$$
\left[ {\begin{array}{*{20}{c}}
{{X_c}}\\
{{Y_c}}\\
{{Z_c}}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{{r_{11}}}&{{r_{12}}}&{{r_{13}}}\\
{{r_{21}}}&{{r_{22}}}&{{r_{23}}}\\
{{r_{31}}}&{{r_{32}}}&{{r_{33}}}
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
{{X_W}}\\
{{Y_W}}\\
{{Z_W}}
\end{array}} \right] + \left[ {\begin{array}{*{20}{c}}
{{T_x}}\\
{{T_y}}\\
{{T_z}}
\end{array}} \right]
$$
為了將**旋轉矩陣**和**平移矩陣**兩個矩陣形式統一,需要引入齊次座標表示形式:
$$
\underbrace {\left[ {\begin{array}{*{20}{c}}
{{X_C}}\\
{{Y_C}}\\
{{Z_C}}\\
1
\end{array}} \right]}_{相機座標系} = \underbrace {\left[ {\begin{array}{*{20}{c}}
{{R_{3 \times 3}}}&{{T_{3 \times 1}}}\\
0&1
\end{array}} \right]}_{剛體變換}\underbrace {\left[ {\begin{array}{*{20}{c}}
{{X_W}}\\
{{Y_W}}\\
{{Z_W}}\\
1
\end{array}} \right]}_{世界座標系}
$$
### 2)相機座標系 -> 影象座標系
從**相機座標系** $[X_C,Y_C, Z_C,1]^T$ 到 **影象座標系** $[x,y]^T$(成像平面) 的變換是個相似三角形變換,推導如下:
|
|
| :----------------------------------------------------------: |
| **圖3 世界座標系 -> 相機座標系(剛體變換)** |
假設該點世界座標系為 $[X_W,Y_W,Z_W]^T$,世界座標系到相機座標系的變換是一個**剛體變換**,那麼同樣的該點,在相機座標系下的座標 $[X_C,Y_C,Z_C]^T$ 如下:
$$
\left[ {\begin{array}{*{20}{c}}
{{X_c}}\\
{{Y_c}}\\
{{Z_c}}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{{r_{11}}}&{{r_{12}}}&{{r_{13}}}\\
{{r_{21}}}&{{r_{22}}}&{{r_{23}}}\\
{{r_{31}}}&{{r_{32}}}&{{r_{33}}}
\end{array}} \right]\left[ {\begin{array}{*{20}{c}}
{{X_W}}\\
{{Y_W}}\\
{{Z_W}}
\end{array}} \right] + \left[ {\begin{array}{*{20}{c}}
{{T_x}}\\
{{T_y}}\\
{{T_z}}
\end{array}} \right]
$$
為了將**旋轉矩陣**和**平移矩陣**兩個矩陣形式統一,需要引入齊次座標表示形式:
$$
\underbrace {\left[ {\begin{array}{*{20}{c}}
{{X_C}}\\
{{Y_C}}\\
{{Z_C}}\\
1
\end{array}} \right]}_{相機座標系} = \underbrace {\left[ {\begin{array}{*{20}{c}}
{{R_{3 \times 3}}}&{{T_{3 \times 1}}}\\
0&1
\end{array}} \right]}_{剛體變換}\underbrace {\left[ {\begin{array}{*{20}{c}}
{{X_W}}\\
{{Y_W}}\\
{{Z_W}}\\
1
\end{array}} \right]}_{世界座標系}
$$
### 2)相機座標系 -> 影象座標系
從**相機座標系** $[X_C,Y_C, Z_C,1]^T$ 到 **影象座標系** $[x,y]^T$(成像平面) 的變換是個相似三角形變換,推導如下:
| 

 1. **世界座標系到相機座標系**:
$$
\underbrace {\left[ {\begin{array}{*{20}{c}}
{{X_C}}\\
{{Y_C}}\\
{{Z_C}}\\
1
\end{array}} \right]}_{相機座標系} = \underbrace {\left[ {\begin{array}{*{20}{c}}
{{R_{3 \times 3}}}&{{T_{3 \times 1}}}\\
0&1
\end{array}} \right]}_{剛體變換}\underbrace {\left[ {\begin{array}{*{20}{c}}
{{X_W}}\\
{{Y_W}}\\
{{Z_W}}\\
1
\end{array}} \right]}_{世界座標系}
$$
2. **相機座標系到影象座標系**:
$$
{Z_c}\underbrace {\left[ {\begin{array}{*{20}{c}}
x\\
y\\
1
\end{array}} \right]}_{\rm{影象座標系}} = \underbrace {\left[ {\begin{array}{*{20}{c}}
f&0&0&0\\
0&f&0&0\\
0&0&1&0
\end{array}} \right]}_{相似三角}\underbrace {\left[ {\begin{array}{*{20}{c}}
{{X_C}}\\
{{Y_C}}\\
{{Z_C}}\\
1
\end{array}} \right]}_{相機座標系}
$$
3. **影象座標系到畫素座標系**:
$$
\underbrace {\left[ {\begin{array}{*{20}{c}}
u\\
v\\
1
\end{array}} \right]}_{畫素座標系} = \underbrace {\left[ {\begin{array}{*{20}{c}}
{\frac{1}{{dx}}}&0&{{u_0}}\\
0&{\frac{1}{{dy}}}&{{v_0}}\\
0&0&1
\end{array}} \right]}_{平移+縮放}\underbrace {\left[ {\begin{array}{*{20}{c}}
x\\
y\\
1
\end{array}} \right]}_{影象座標系}
$$
將之前所有的變換合併,可以得到:
$$
{Z_c}\underbrace {\left[ {\begin{array}{*{20}{c}}
u\\
v\\
1
\end{array}} \right]}_{畫素座標系} = \underbrace {\left[ {\begin{array}{*{20}{c}}
{\frac{1}{{dx}}}&0&{{u_0}}\\
0&{\frac{1}{{dy}}}&{{v_0}}\\
0&0&1
\end{array}} \right]}_{03 \ 平移+縮放}\underbrace {\left[ {\begin{array}{*{20}{c}}
f&0&0&0\\
0&f&0&0\\
0&0&1&0
\end{array}} \right]}_{02\ 相似三角形}\underbrace {\left[ {\begin{array}{*{20}{c}}
{{R_{3 \times 3}}}&{{T_{3 \times 1}}}\\
0&1
\end{array}} \right]}_{01 \ 剛體變換}\underbrace {\left[ {\begin{array}{*{20}{c}}
{{X_W}}\\
{{Y_W}}\\
{{Z_W}}\\
1
\end{array}} \right]}_{世界座標系}
$$
將它們相乘後化簡:
$$
{Z_c}\underbrace {\left[ {\begin{array}{*{20}{c}}
u \\
v \\
1
\end{array}} \right]}_{畫素座標系} = \underbrace {\left[ {\begin{array}{*{20}{c}}
{{f_x}}&0&{{u_0}} \\
0&{{f_y}}&{{v_0}} \\
0&0&1
\end{array}} \right]}_{M1:內參}\underbrace {\left[ {\begin{array}{*{20}{c}}
{{R_{3 \times 3}}}&{{T_{3 \times 1}}}
\end{array}} \right]}_{M2:外參}\underbrace {\left[ {\begin{array}{*{20}{c}}
{{X_W}} \\
{{Y_W}} \\
{{Z_W}} \\
1
\end{array}} \right]}_{世界座標系}
$$
以上是理想情況下世界座標系到畫素座標系的轉換,而由於相機制造工藝的原因,其成像過程中難免存在著畸變,在後續構建精確的三維重建演算法前,我們要對相機的畸變進行矯正,以提高演算法重建的精度,這一步驟也稱為**相機標定**。
## 02 考慮畸變情況下相機成像模型
相機畸變主要有兩種型別:**徑向畸變** 和 **切向畸變**,我們分別介紹這兩種情況。
### 1)徑向畸變
> **原因**:在相機制造過程中,很難保證鏡頭的厚度完全均勻,由於製造工藝的原因,通常為這種情況為中間厚、邊緣薄,因而光線在遠離透鏡中心的地方,會發生更大程度的扭曲,這種現象在魚眼相機(桶形畸變)中尤為明顯。
徑向畸變主要有兩種型別:**枕型畸變**和**桶型畸變**,示意圖如下:
|
1. **世界座標系到相機座標系**:
$$
\underbrace {\left[ {\begin{array}{*{20}{c}}
{{X_C}}\\
{{Y_C}}\\
{{Z_C}}\\
1
\end{array}} \right]}_{相機座標系} = \underbrace {\left[ {\begin{array}{*{20}{c}}
{{R_{3 \times 3}}}&{{T_{3 \times 1}}}\\
0&1
\end{array}} \right]}_{剛體變換}\underbrace {\left[ {\begin{array}{*{20}{c}}
{{X_W}}\\
{{Y_W}}\\
{{Z_W}}\\
1
\end{array}} \right]}_{世界座標系}
$$
2. **相機座標系到影象座標系**:
$$
{Z_c}\underbrace {\left[ {\begin{array}{*{20}{c}}
x\\
y\\
1
\end{array}} \right]}_{\rm{影象座標系}} = \underbrace {\left[ {\begin{array}{*{20}{c}}
f&0&0&0\\
0&f&0&0\\
0&0&1&0
\end{array}} \right]}_{相似三角}\underbrace {\left[ {\begin{array}{*{20}{c}}
{{X_C}}\\
{{Y_C}}\\
{{Z_C}}\\
1
\end{array}} \right]}_{相機座標系}
$$
3. **影象座標系到畫素座標系**:
$$
\underbrace {\left[ {\begin{array}{*{20}{c}}
u\\
v\\
1
\end{array}} \right]}_{畫素座標系} = \underbrace {\left[ {\begin{array}{*{20}{c}}
{\frac{1}{{dx}}}&0&{{u_0}}\\
0&{\frac{1}{{dy}}}&{{v_0}}\\
0&0&1
\end{array}} \right]}_{平移+縮放}\underbrace {\left[ {\begin{array}{*{20}{c}}
x\\
y\\
1
\end{array}} \right]}_{影象座標系}
$$
將之前所有的變換合併,可以得到:
$$
{Z_c}\underbrace {\left[ {\begin{array}{*{20}{c}}
u\\
v\\
1
\end{array}} \right]}_{畫素座標系} = \underbrace {\left[ {\begin{array}{*{20}{c}}
{\frac{1}{{dx}}}&0&{{u_0}}\\
0&{\frac{1}{{dy}}}&{{v_0}}\\
0&0&1
\end{array}} \right]}_{03 \ 平移+縮放}\underbrace {\left[ {\begin{array}{*{20}{c}}
f&0&0&0\\
0&f&0&0\\
0&0&1&0
\end{array}} \right]}_{02\ 相似三角形}\underbrace {\left[ {\begin{array}{*{20}{c}}
{{R_{3 \times 3}}}&{{T_{3 \times 1}}}\\
0&1
\end{array}} \right]}_{01 \ 剛體變換}\underbrace {\left[ {\begin{array}{*{20}{c}}
{{X_W}}\\
{{Y_W}}\\
{{Z_W}}\\
1
\end{array}} \right]}_{世界座標系}
$$
將它們相乘後化簡:
$$
{Z_c}\underbrace {\left[ {\begin{array}{*{20}{c}}
u \\
v \\
1
\end{array}} \right]}_{畫素座標系} = \underbrace {\left[ {\begin{array}{*{20}{c}}
{{f_x}}&0&{{u_0}} \\
0&{{f_y}}&{{v_0}} \\
0&0&1
\end{array}} \right]}_{M1:內參}\underbrace {\left[ {\begin{array}{*{20}{c}}
{{R_{3 \times 3}}}&{{T_{3 \times 1}}}
\end{array}} \right]}_{M2:外參}\underbrace {\left[ {\begin{array}{*{20}{c}}
{{X_W}} \\
{{Y_W}} \\
{{Z_W}} \\
1
\end{array}} \right]}_{世界座標系}
$$
以上是理想情況下世界座標系到畫素座標系的轉換,而由於相機制造工藝的原因,其成像過程中難免存在著畸變,在後續構建精確的三維重建演算法前,我們要對相機的畸變進行矯正,以提高演算法重建的精度,這一步驟也稱為**相機標定**。
## 02 考慮畸變情況下相機成像模型
相機畸變主要有兩種型別:**徑向畸變** 和 **切向畸變**,我們分別介紹這兩種情況。
### 1)徑向畸變
> **原因**:在相機制造過程中,很難保證鏡頭的厚度完全均勻,由於製造工藝的原因,通常為這種情況為中間厚、邊緣薄,因而光線在遠離透鏡中心的地方,會發生更大程度的扭曲,這種現象在魚眼相機(桶形畸變)中尤為明顯。
徑向畸變主要有兩種型別:**枕型畸變**和**桶型畸變**,示意圖如下:
|  |
|  |
| :----------------------------------------------------------: | :----------------------------------------------------------: |
|
|
| :----------------------------------------------------------: | :----------------------------------------------------------: |
|  |
|  |
| **桶型畸變** | **枕形畸變** |
它們可以由 $k_1,k_2$ 構成的下列數學公式描述:
$$
\left[ {\begin{array}{*{20}{c}}
{x'}\\
{y'}
\end{array}} \right] = (1 + {k_1}{r^2} + {k_2}{r^4} + {k_3}{r^6})\left[ {\begin{array}{*{20}{c}}
x\\
y
\end{array}} \right]
$$
其中:
- $r$ 為曲率半徑,有:$r^2 =x^2 + y^2$;
- $k_1,k_2,k_3$ 為徑向畸變係數;
- $x, y$ 為發生畸變后角點的座標,也就是我們實際看到的;
- $x',y'$ 為畸變矯正,也就是去除畸變後的正確座標;
> 注:這裡無論是 $x, y,x',y'$,其均為歸一化平面上角點的座標。
通常:我們只用 $k_1,k_2$ 來矯正相機,對於畸變較小的影象中心區域,主要是 $k_1$ 在起作用,對於畸變較大的影象邊緣區域,主要是 $k_2$ 在起作用,而對於魚眼相機這類廣角相機,我們才會用 $k_3$。需要注意的是,這裡並不是用的係數越多,整個矯正結果越精確,我們應該考慮相機的實際情況。
### 2)切向畸變
> **原因**:切向畸變產生的原因在於相機在製造過程中,成像平面與透鏡平面不平行,產生了透視變換。
|
| **桶型畸變** | **枕形畸變** |
它們可以由 $k_1,k_2$ 構成的下列數學公式描述:
$$
\left[ {\begin{array}{*{20}{c}}
{x'}\\
{y'}
\end{array}} \right] = (1 + {k_1}{r^2} + {k_2}{r^4} + {k_3}{r^6})\left[ {\begin{array}{*{20}{c}}
x\\
y
\end{array}} \right]
$$
其中:
- $r$ 為曲率半徑,有:$r^2 =x^2 + y^2$;
- $k_1,k_2,k_3$ 為徑向畸變係數;
- $x, y$ 為發生畸變后角點的座標,也就是我們實際看到的;
- $x',y'$ 為畸變矯正,也就是去除畸變後的正確座標;
> 注:這裡無論是 $x, y,x',y'$,其均為歸一化平面上角點的座標。
通常:我們只用 $k_1,k_2$ 來矯正相機,對於畸變較小的影象中心區域,主要是 $k_1$ 在起作用,對於畸變較大的影象邊緣區域,主要是 $k_2$ 在起作用,而對於魚眼相機這類廣角相機,我們才會用 $k_3$。需要注意的是,這裡並不是用的係數越多,整個矯正結果越精確,我們應該考慮相機的實際情況。
### 2)切向畸變
> **原因**:切向畸變產生的原因在於相機在製造過程中,成像平面與透鏡平面不平行,產生了透視變換。

 這種畸變可以由以下公式描述,它也與距離影象中心的距離半徑有關:
$$
\left[ {\begin{array}{*{20}{c}}
x'\\
y'
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{2{p_1}xy + {p_2}\left( {{r^2} + 2{x^2}} \right)}\\
{2{p_2}xy + {p_1}\left( {{r^2} + 2{y^2}} \right)}
\end{array}} \right]
$$
其中:$p_1,p_2$ 稱為切向畸變矯正係數,其它的含義與徑向畸變中公式相同。
### 3)合併考慮畸變
> 原因:其實也很簡單,兩種畸變是同時發生在成像過程中的,發生的原因也是相互獨立的,而且也都是關於距離的表示式,你似乎也找不到更好的方式來綜合考慮這兩種誤差,實踐證明,這種合併考慮畸變的情況效果還不錯。
將徑向畸變和切向畸變合併,只需要將兩個畸變矯正直接加起來即可,公式如下:
$$
\left[ {\begin{array}{*{20}{c}}
{x'}\\
{y'}
\end{array}} \right] = \underbrace {\left( {1 + {k_1}{r^2} + {k_2}{r^4} + {k_3}{r^6}} \right)\left[ {\begin{array}{*{20}{c}}
x\\
y
\end{array}} \right]}_{徑向畸變} + \underbrace {\left[ {\begin{array}{*{20}{c}}
{2{p_1}xy + {p_2}\left( {{r^2} + 2{x^2}} \right)}\\
{2{p_2}xy + p1\left( {{r^2} + 2{y^2}} \right)}
\end{array}} \right]}_{切向畸變}
$$
其中:
- $k_1,k_2,k_3$ 為徑向畸變係數;
- $p_1,p_2$ 為切向畸變係數;
不過在此之前,我們特別注意一點,相機畸變現象發生的位置:
- **世界座標系 -> 相機座標系**,剛體變換,不存在畸變現象;
- **相機座標系 -> 影象座標系**,也就是成像過程,理想情況下是相似三角形,但實際由於相機制造、裝配的原因,成像過程存在畸變現象;
- **影象座標系 -> 畫素座標系**,座標原點、單位不同,僅僅平移與縮放,不存在畸變現象;
## 03 成像過程總結
現在,我們將這些公式進行整理,假設:
- 某點世界座標系為$P(X_W,Y_W,Z_W)$;
- 對應的實際得到的畫素座標系為 $P(u,v)$(未矯正的);
- 正確的畫素座標為 $P(u',v')$;
- 假設我們已知畸變係數 $k_1,k_2,k_3,p_1,p_2$;
那麼從世界座標系 $P(X_W,Y_W,Z_W)$ 到正確的畫素座標系 $P(u',v')$ 的推導如下,對於畫素座標系下某點 $P(u,v)$,有:
1. **畫素座標系 -> 歸一化座標系**
這個變換僅僅是平移與縮放,不存在畸變,因而只需要一個逆變換,歸一化座標 $P=(x,y)^T$ 推導如下:
$$
\begin{array}{c}
\underbrace {\left[ {\begin{array}{*{20}{c}}
u\\
v\\
1
\end{array}} \right]}_{畫素座標} = \underbrace {\left[ {\begin{array}{*{20}{c}}
{\frac{1}{{dx}}}&0&{{u_0}}\\
0&{\frac{1}{{dy}}}&{{v_0}}\\
0&0&1
\end{array}} \right]}_{平移+縮放}\underbrace {\left( {\underbrace {\left[ {\begin{array}{*{20}{c}}
x\\
y\\
{1/f}
\end{array}} \right]}_{歸一化座標} \times f} \right)}_{影象座標}
\\
\Downarrow
\\
\underbrace {\left[ {\begin{array}{*{20}{c}}
x\\
y\\
{1/f}
\end{array}} \right]}_{歸一化座標} = \underbrace {\left( {{{\left[ {\begin{array}{*{20}{c}}
{\frac{1}{{dx}}}&0&{{u_0}}\\
0&{\frac{1}{{dy}}}&{{v_0}}\\
0&0&1
\end{array}} \right]}^{ - 1}}\underbrace {\left[ {\begin{array}{*{20}{c}}
u\\
v\\
1
\end{array}} \right]}_{畫素座標}} \right)}_{影象座標}/f
\end{array}
$$
2. **歸一化座標系(帶畸變的) -> 歸一化座標系(畸變矯正後)**
在前一成像過程,也就是相機座標系到歸一化平面透射中,相機發生了畸變,因而我們需要將實際的歸一化座標 $P=(x,y)^T$ 糾正到理想的無畸變歸一化座標 $P=(x',y')^T$:
$$
\left[ {\begin{array}{*{20}{c}}
{x'}\\
{y'}\\
{1/f}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{\left( {1 + {k_1}{r^2} + {k_2}{r^4} + {k_3}{r^6}} \right)x + 2{p_1}xy + {p_2}\left( {{r^2} + 2{x^2}} \right)}\\
{\left( {1 + {k_1}{r^2} + {k_2}{r^4} + {k_3}{r^6}} \right)y + 2{p_2}xy + {p_1}\left( {{r^2} + 2{y^2}} \right)}\\
{1/f}
\end{array}} \right]
$$
3. **歸一化座標系(理想)-> 相機座標系**
理想的無畸變歸一化座標 $P=(x',y')$ 到相機座標系,它們是相似三角形關係:
$$
{Z_c}\underbrace {\left( {\underbrace {\left[ {\begin{array}{*{20}{c}}
{x'}\\
{y'}\\
1/f
\end{array}} \right]}_{歸一化座標系(準確)} \cdot f} \right)}_{影象座標}
= \underbrace {\left[ {\begin{array}{*{20}{c}}
f&0&0&0\\
0&f&0&0\\
0&0&1&0
\end{array}} \right]}_{相似三角形}\underbrace {\left[ {\begin{array}{*{20}{c}}
{{X_C}}\\
{{Y_C}}\\
{{Z_C}}\\
1
\end{array}} \right]}_{相機座標} \\
\Downarrow
\\
\left[ {\begin{array}{*{20}{c}}
{{X_c}}\\
{{Y_c}}\\
{{Z_c}}\\
1
\end{array}} \right] = f \cdot {Z_c} \cdot {\left[ {\begin{array}{*{20}{c}}
f&0&0&0\\
0&f&0&0\\
0&0&1&0
\end{array}} \right]^{ - 1}}\left[ {\begin{array}{*{20}{c}}
{x'}\\
{y'}\\
{1/f}
\end{array}} \right]
$$
注:這裡 $3 \times 4$ 矩陣的逆是偽逆。
4. **相機座標系 -> 世界座標系**
相機座標系到世界座標系,僅僅是之前剛體變換的反變換:
$$
\underbrace {\left[ {\begin{array}{*{20}{c}}
{{X_C}}\\
{{Y_C}}\\
{{Z_C}}\\
1
\end{array}} \right]}_{相機座標系} = \underbrace {\left[ {\begin{array}{*{20}{c}}
{{R_{3 \times 3}}}&{{T_{3 \times 1}}}\\
0&1
\end{array}} \right]}_{剛體變換}\underbrace {\left[ {\begin{array}{*{20}{c}}
{{X_W}}\\
{{Y_W}}\\
{{Z_W}}\\
1
\end{array}} \right]}_{世界座標系}
\\
\Downarrow
\\
\left[ {\begin{array}{*{20}{c}}
{{X_W}}\\
{{Y_W}}\\
{{Z_W}}\\
1
\end{array}} \right] = {\left[ {\begin{array}{*{20}{c}}
{{R_{3 \times 3}}}&{{T_{3 \times 1}}}\\
0&1
\end{array}} \right]^{ - 1}}\left[ {\begin{array}{*{20}{c}}
{{X_C}}\\
{{Y_c}}\\
{{Z_c}}\\
1
\end{array}} \right]
$$
所以,我們只需要將上述的四個公式合併起來即可,畫素座標系$P=(u,v)$轉換到世界座標系 $P=(X_W,Y_W,Z_W)$。
## 04 思考問題
現在的問題是,我們如何求得這些畸變係數 $k_1,k_2,k_3,p_1,p_2$?得到這些係數之後,我們就能建立畫素座標系與世界座標系的對映。這個問題可以由**張正友標定法**來實現。
> 對於張正友標定法的原理,略微有些複雜,在下一節推送中,我們從它的實現開始講起,然後如果你們有興趣,可以看我們的拓展閱讀《張正友標定法數學基礎及原理推導》。
先回過頭來看前面的式子,我們可以看到,即使考慮了畸變,從畫素座標系到世界座標系的轉換,其實還是一些乘法運算,但是這裡有兩個問題需要大家思考:
### 1)問題一
對於考慮了畸變的相機模型,世界座標系與畫素座標系之間的轉換公式,其實是存在一個問題的:不能寫成完全矩陣$x,y$ 的乘法形式。因為相機模型的切向畸變部分包含非線性項 $xy,x^2,y^2$:
$$
\left[ {\begin{array}{*{20}{c}}
{x'}\\
{y'}
\end{array}} \right] = \underbrace {\left( {1 + {k_1}{r^2} + {k_2}{r^4} + {k_3}{r^6}} \right)\left[ {\begin{array}{*{20}{c}}
x\\
y
\end{array}} \right]}_{徑向畸變} + \underbrace {\left[ {\begin{array}{*{20}{c}}
{2{p_1}xy + {p_2}\left( {{r^2} + 2{x^2}} \right)}\\
{2{p_2}xy + p1\left( {{r^2} + 2{y^2}} \right)}
\end{array}} \right]}_{切向畸變}
$$
> 有人說,這樣似乎也沒什麼問題嘛,無非是計算速度慢一點而已,但事情不是這樣的,矩陣方程裡存在著非線性項,而且還有一個加法,我們那些關於方程組解、求特徵值、正定、半正定、正交這些理論武器,全部都失去作用了。
事實上,一些質量較好的工業相機,切向畸變都是很小的(話說,相機都不準,你拿它做什麼精確的三維重建…),張正友標定法在初始的時候即假設相機不存在徑向畸變(之後會求),也就是 $p_1,p_2$ 都等於零,另外同樣$k3=0$。這樣的好處在於,考慮畸變的相機模型,在初期跟理想模型的差別在於乘以一個常數項,整個式子就可以寫為一個單應性矩陣的形式,方便我們對方程組進行優化:
$$
s\tilde m = A\left[ {\begin{array}{*{20}{c}}
{{R_{3 \times 3}}}&{{T_{3 \times 1}}}
\end{array}} \right]\tilde M
$$
其中:
- $s$ 稱為尺度因子;
- $\tilde m $ 為畫素座標系,$\tilde M $ 為世界座標系;
- $A$ 為單應性矩陣;
- $[R_{3 \times 3} \ T_{3\times1}]$ 是外參矩陣;
### 2)問題二
還有個問題,假設我們得到了這些畸變係數,能否由畫素座標系推導到世界座標系?事實上是不能的,比如下面這種圖:
|
這種畸變可以由以下公式描述,它也與距離影象中心的距離半徑有關:
$$
\left[ {\begin{array}{*{20}{c}}
x'\\
y'
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{2{p_1}xy + {p_2}\left( {{r^2} + 2{x^2}} \right)}\\
{2{p_2}xy + {p_1}\left( {{r^2} + 2{y^2}} \right)}
\end{array}} \right]
$$
其中:$p_1,p_2$ 稱為切向畸變矯正係數,其它的含義與徑向畸變中公式相同。
### 3)合併考慮畸變
> 原因:其實也很簡單,兩種畸變是同時發生在成像過程中的,發生的原因也是相互獨立的,而且也都是關於距離的表示式,你似乎也找不到更好的方式來綜合考慮這兩種誤差,實踐證明,這種合併考慮畸變的情況效果還不錯。
將徑向畸變和切向畸變合併,只需要將兩個畸變矯正直接加起來即可,公式如下:
$$
\left[ {\begin{array}{*{20}{c}}
{x'}\\
{y'}
\end{array}} \right] = \underbrace {\left( {1 + {k_1}{r^2} + {k_2}{r^4} + {k_3}{r^6}} \right)\left[ {\begin{array}{*{20}{c}}
x\\
y
\end{array}} \right]}_{徑向畸變} + \underbrace {\left[ {\begin{array}{*{20}{c}}
{2{p_1}xy + {p_2}\left( {{r^2} + 2{x^2}} \right)}\\
{2{p_2}xy + p1\left( {{r^2} + 2{y^2}} \right)}
\end{array}} \right]}_{切向畸變}
$$
其中:
- $k_1,k_2,k_3$ 為徑向畸變係數;
- $p_1,p_2$ 為切向畸變係數;
不過在此之前,我們特別注意一點,相機畸變現象發生的位置:
- **世界座標系 -> 相機座標系**,剛體變換,不存在畸變現象;
- **相機座標系 -> 影象座標系**,也就是成像過程,理想情況下是相似三角形,但實際由於相機制造、裝配的原因,成像過程存在畸變現象;
- **影象座標系 -> 畫素座標系**,座標原點、單位不同,僅僅平移與縮放,不存在畸變現象;
## 03 成像過程總結
現在,我們將這些公式進行整理,假設:
- 某點世界座標系為$P(X_W,Y_W,Z_W)$;
- 對應的實際得到的畫素座標系為 $P(u,v)$(未矯正的);
- 正確的畫素座標為 $P(u',v')$;
- 假設我們已知畸變係數 $k_1,k_2,k_3,p_1,p_2$;
那麼從世界座標系 $P(X_W,Y_W,Z_W)$ 到正確的畫素座標系 $P(u',v')$ 的推導如下,對於畫素座標系下某點 $P(u,v)$,有:
1. **畫素座標系 -> 歸一化座標系**
這個變換僅僅是平移與縮放,不存在畸變,因而只需要一個逆變換,歸一化座標 $P=(x,y)^T$ 推導如下:
$$
\begin{array}{c}
\underbrace {\left[ {\begin{array}{*{20}{c}}
u\\
v\\
1
\end{array}} \right]}_{畫素座標} = \underbrace {\left[ {\begin{array}{*{20}{c}}
{\frac{1}{{dx}}}&0&{{u_0}}\\
0&{\frac{1}{{dy}}}&{{v_0}}\\
0&0&1
\end{array}} \right]}_{平移+縮放}\underbrace {\left( {\underbrace {\left[ {\begin{array}{*{20}{c}}
x\\
y\\
{1/f}
\end{array}} \right]}_{歸一化座標} \times f} \right)}_{影象座標}
\\
\Downarrow
\\
\underbrace {\left[ {\begin{array}{*{20}{c}}
x\\
y\\
{1/f}
\end{array}} \right]}_{歸一化座標} = \underbrace {\left( {{{\left[ {\begin{array}{*{20}{c}}
{\frac{1}{{dx}}}&0&{{u_0}}\\
0&{\frac{1}{{dy}}}&{{v_0}}\\
0&0&1
\end{array}} \right]}^{ - 1}}\underbrace {\left[ {\begin{array}{*{20}{c}}
u\\
v\\
1
\end{array}} \right]}_{畫素座標}} \right)}_{影象座標}/f
\end{array}
$$
2. **歸一化座標系(帶畸變的) -> 歸一化座標系(畸變矯正後)**
在前一成像過程,也就是相機座標系到歸一化平面透射中,相機發生了畸變,因而我們需要將實際的歸一化座標 $P=(x,y)^T$ 糾正到理想的無畸變歸一化座標 $P=(x',y')^T$:
$$
\left[ {\begin{array}{*{20}{c}}
{x'}\\
{y'}\\
{1/f}
\end{array}} \right] = \left[ {\begin{array}{*{20}{c}}
{\left( {1 + {k_1}{r^2} + {k_2}{r^4} + {k_3}{r^6}} \right)x + 2{p_1}xy + {p_2}\left( {{r^2} + 2{x^2}} \right)}\\
{\left( {1 + {k_1}{r^2} + {k_2}{r^4} + {k_3}{r^6}} \right)y + 2{p_2}xy + {p_1}\left( {{r^2} + 2{y^2}} \right)}\\
{1/f}
\end{array}} \right]
$$
3. **歸一化座標系(理想)-> 相機座標系**
理想的無畸變歸一化座標 $P=(x',y')$ 到相機座標系,它們是相似三角形關係:
$$
{Z_c}\underbrace {\left( {\underbrace {\left[ {\begin{array}{*{20}{c}}
{x'}\\
{y'}\\
1/f
\end{array}} \right]}_{歸一化座標系(準確)} \cdot f} \right)}_{影象座標}
= \underbrace {\left[ {\begin{array}{*{20}{c}}
f&0&0&0\\
0&f&0&0\\
0&0&1&0
\end{array}} \right]}_{相似三角形}\underbrace {\left[ {\begin{array}{*{20}{c}}
{{X_C}}\\
{{Y_C}}\\
{{Z_C}}\\
1
\end{array}} \right]}_{相機座標} \\
\Downarrow
\\
\left[ {\begin{array}{*{20}{c}}
{{X_c}}\\
{{Y_c}}\\
{{Z_c}}\\
1
\end{array}} \right] = f \cdot {Z_c} \cdot {\left[ {\begin{array}{*{20}{c}}
f&0&0&0\\
0&f&0&0\\
0&0&1&0
\end{array}} \right]^{ - 1}}\left[ {\begin{array}{*{20}{c}}
{x'}\\
{y'}\\
{1/f}
\end{array}} \right]
$$
注:這裡 $3 \times 4$ 矩陣的逆是偽逆。
4. **相機座標系 -> 世界座標系**
相機座標系到世界座標系,僅僅是之前剛體變換的反變換:
$$
\underbrace {\left[ {\begin{array}{*{20}{c}}
{{X_C}}\\
{{Y_C}}\\
{{Z_C}}\\
1
\end{array}} \right]}_{相機座標系} = \underbrace {\left[ {\begin{array}{*{20}{c}}
{{R_{3 \times 3}}}&{{T_{3 \times 1}}}\\
0&1
\end{array}} \right]}_{剛體變換}\underbrace {\left[ {\begin{array}{*{20}{c}}
{{X_W}}\\
{{Y_W}}\\
{{Z_W}}\\
1
\end{array}} \right]}_{世界座標系}
\\
\Downarrow
\\
\left[ {\begin{array}{*{20}{c}}
{{X_W}}\\
{{Y_W}}\\
{{Z_W}}\\
1
\end{array}} \right] = {\left[ {\begin{array}{*{20}{c}}
{{R_{3 \times 3}}}&{{T_{3 \times 1}}}\\
0&1
\end{array}} \right]^{ - 1}}\left[ {\begin{array}{*{20}{c}}
{{X_C}}\\
{{Y_c}}\\
{{Z_c}}\\
1
\end{array}} \right]
$$
所以,我們只需要將上述的四個公式合併起來即可,畫素座標系$P=(u,v)$轉換到世界座標系 $P=(X_W,Y_W,Z_W)$。
## 04 思考問題
現在的問題是,我們如何求得這些畸變係數 $k_1,k_2,k_3,p_1,p_2$?得到這些係數之後,我們就能建立畫素座標系與世界座標系的對映。這個問題可以由**張正友標定法**來實現。
> 對於張正友標定法的原理,略微有些複雜,在下一節推送中,我們從它的實現開始講起,然後如果你們有興趣,可以看我們的拓展閱讀《張正友標定法數學基礎及原理推導》。
先回過頭來看前面的式子,我們可以看到,即使考慮了畸變,從畫素座標系到世界座標系的轉換,其實還是一些乘法運算,但是這裡有兩個問題需要大家思考:
### 1)問題一
對於考慮了畸變的相機模型,世界座標系與畫素座標系之間的轉換公式,其實是存在一個問題的:不能寫成完全矩陣$x,y$ 的乘法形式。因為相機模型的切向畸變部分包含非線性項 $xy,x^2,y^2$:
$$
\left[ {\begin{array}{*{20}{c}}
{x'}\\
{y'}
\end{array}} \right] = \underbrace {\left( {1 + {k_1}{r^2} + {k_2}{r^4} + {k_3}{r^6}} \right)\left[ {\begin{array}{*{20}{c}}
x\\
y
\end{array}} \right]}_{徑向畸變} + \underbrace {\left[ {\begin{array}{*{20}{c}}
{2{p_1}xy + {p_2}\left( {{r^2} + 2{x^2}} \right)}\\
{2{p_2}xy + p1\left( {{r^2} + 2{y^2}} \right)}
\end{array}} \right]}_{切向畸變}
$$
> 有人說,這樣似乎也沒什麼問題嘛,無非是計算速度慢一點而已,但事情不是這樣的,矩陣方程裡存在著非線性項,而且還有一個加法,我們那些關於方程組解、求特徵值、正定、半正定、正交這些理論武器,全部都失去作用了。
事實上,一些質量較好的工業相機,切向畸變都是很小的(話說,相機都不準,你拿它做什麼精確的三維重建…),張正友標定法在初始的時候即假設相機不存在徑向畸變(之後會求),也就是 $p_1,p_2$ 都等於零,另外同樣$k3=0$。這樣的好處在於,考慮畸變的相機模型,在初期跟理想模型的差別在於乘以一個常數項,整個式子就可以寫為一個單應性矩陣的形式,方便我們對方程組進行優化:
$$
s\tilde m = A\left[ {\begin{array}{*{20}{c}}
{{R_{3 \times 3}}}&{{T_{3 \times 1}}}
\end{array}} \right]\tilde M
$$
其中:
- $s$ 稱為尺度因子;
- $\tilde m $ 為畫素座標系,$\tilde M $ 為世界座標系;
- $A$ 為單應性矩陣;
- $[R_{3 \times 3} \ T_{3\times1}]$ 是外參矩陣;
### 2)問題二
還有個問題,假設我們得到了這些畸變係數,能否由畫素座標系推導到世界座標系?事實上是不能的,比如下面這種圖:
|  |
|  |
| :----------------------------------------------------------: | :----------------------------------------------------------: |
| 圖a 單目相機失真 | 圖2 單目相機模型 |
光心 $O_c$ 與$P(X_C,Y_C,Z_C)$ 的整條連線上的三維點,在成像平面的像點均在點 $p(x,y)$ 上。所以在單目相機的標定方法中,甚至不需要知道棋盤格的實際大小也能完成相機的
|
| :----------------------------------------------------------: | :----------------------------------------------------------: |
| 圖a 單目相機失真 | 圖2 單目相機模型 |
光心 $O_c$ 與$P(X_C,Y_C,Z_C)$ 的整條連線上的三維點,在成像平面的像點均在點 $p(x,y)$ 上。所以在單目相機的標定方法中,甚至不需要知道棋盤格的實際大小也能完成相機的
