題目描述

小T 是一名質量監督員，最近負責檢驗一批礦產的質量。這批礦產共有 n 個礦石，從 1到n 逐一編號，每個礦石都有自己的重量 wi 以及價值vi 。檢驗礦產的流程是：

1 、給定m 個區間[Li,Ri]；

2 、選出一個參數 W；

3 、對於一個區間[Li,Ri]，計算礦石在這個區間上的檢驗值Yi：

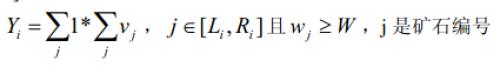
這批礦產的檢驗結果Y 為各個區間的檢驗值之和。即：Y1+Y2...+Ym

若這批礦產的檢驗結果與所給標準值S 相差太多，就需要再去檢驗另一批礦產。小T

不想費時間去檢驗另一批礦產，所以他想通過調整參數W 的值，讓檢驗結果盡可能的靠近

標準值S，即使得S-Y 的絕對值最小。請你幫忙求出這個最小值。

輸入輸出格式

輸入格式：

輸入文件qc.in 。

第一行包含三個整數n，m，S，分別表示礦石的個數、區間的個數和標準值。

接下來的n 行，每行2個整數，中間用空格隔開，第i+1 行表示 i 號礦石的重量 wi 和價值vi。

接下來的m 行，表示區間，每行2 個整數，中間用空格隔開，第i+n+1 行表示區間[Li,Ri]的兩個端點Li 和Ri。註意：不同區間可能重合或相互重疊。

輸出格式：

輸出文件名為qc.out。

輸出只有一行，包含一個整數，表示所求的最小值。

輸入輸出樣例

5 3 15 
1 5 
2 5 
3 5 
4 5 
5 5 
1 5 
2 4 
3 3 

10

說明

【輸入輸出樣例說明】

當W 選4 的時候，三個區間上檢驗值分別為 20、5 、0 ，這批礦產的檢驗結果為 25，此

時與標準值S 相差最小為10。

【數據範圍】

對於10% 的數據，有 1 ≤n ，m≤10；

對於30% 的數據，有 1 ≤n ，m≤500 ；

對於50% 的數據，有 1 ≤n ，m≤5,000；

對於70% 的數據，有 1 ≤n ，m≤10,000 ；

對於100%的數據，有 1 ≤n ，m≤200,000，0 < wi, vi≤10^6，0 < S≤10^12，1 ≤Li ≤Ri ≤n 。

二分答案，開long long

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
#define M 800000
#define LL long long

int n,m;
LL S;
int w[M],v[M],L[M],R[M];
LL num[M],sum[M];
int l=1e7,r=0;

LL min(LL a,LL b){return a > b ? b : a;}

int max(int a,int b){return a > b ? a : b;}

LL check(int x)
{
    LL y=0,t=0,yy=0;
    for(int i=1;i<=n;i++)
    {
        sum[i]=sum[i-1];
        num[i]=num[i-1];
        if(w[i]>=x) sum[i]+=v[i],num[i]++;
    }
    for(int i=1;i<=m;i++)
    {
        LL ss=sum[R[i]]-sum[L[i]-1];
        LL nn=num[R[i]]-num[L[i]-1];
        yy+=ss*nn;
    }
    return yy;
}

int main()
{
    scanf("%d%d%lld",&n,&m,&S);
    for(int i=1;i<=n;i++)
    scanf("%d%d",&w[i],&v[i]),
    r=max(r,w[i]),l=min(l,w[i]);
    for(int i=1;i<=m;i++)
    scanf("%d%d",&L[i],&R[i]);
    int mid;
    LL ans=100000000000;
    while(l<=r)
    {
        mid=(l+r)>>1;
        LL tmp=check(mid);
        if(tmp<S) r=mid-1;
        else if(tmp>S)l=mid+1;
        else if(tmp==S) {puts("0");return 0;}
        LL t=S-tmp;
        if(t<0)t=-t;
        ans=min(ans,t);
    }
    printf("%lld\n",ans);
    return 0;
}

luogu P1314 聰明的質監員