小T 是一名質量監督員，最近負責檢驗一批礦產的質量。這批礦產共有 nn 個礦石，從 11到nn逐一編號，每個礦石都有自己的重量 w_iwi? 以及價值v_ivi? 。檢驗礦產的流程是：

1 、給定mm個區間[L_i,R_i][Li?,Ri?]；

2 、選出一個參數WW；

3 、對於一個區間[L_i,R_i][Li?,Ri?]，計算礦石在這個區間上的檢驗值Y_iYi?：

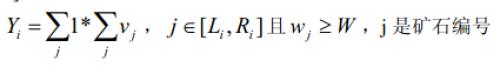
這批礦產的檢驗結果YY 為各個區間的檢驗值之和。即：Y_1+Y_2...+Y_mY1?+Y2?...+Ym?

若這批礦產的檢驗結果與所給標準值SS 相差太多，就需要再去檢驗另一批礦產。小T不想費時間去檢驗另一批礦產，所以他想通過調整參數W 的值，讓檢驗結果盡可能的靠近標準值SS，即使得S-YS−Y 的絕對值最小。請你幫忙求出這個最小值。

11年的day2T2，需要一點思維和數學

首先我遇到的第一個難點是看不懂那個表達式

其實很簡單，意思就是在這個區間內，重量小於W的東西的價值的和，再乘上其數量

然後我們會發現，Y的值是由W的值來決定的，隨著W的增大而減小

要求的又是極值，所以自然而然的想到二分，

接下來就是如何判斷了，因為是區間求和，而有時多個區間，肯定不能暴力

要用到的是前綴和優化，區間和和區間個數都能求

時間復雜度就是O（mlogw）的

別忘了開long long

下面給出代碼：

#include<iostream>
#include<cstdio>
#include
 
<cstdlib>
#include<cstring>
#include<string>
#include<cmath>
#include<algorithm>
using namespace std;
inline long long rd(){
    long long x=0,f=1;
    char ch=getchar();
    for(;!isdigit(ch);ch=getchar()) if(ch==‘-‘) f=-1;
    for(;isdigit(ch);ch=getchar()) x=x*10
 
+ch-‘0‘;
    return x*f;
}
inline void write(long long x){
    if(x<0) putchar(‘-‘),x=-x;
    if(x>9) write(x/10);
    putchar(x%10+‘0‘);
    return ;
}
long long n,m,s;
long long w[1000006],v[1000006];
long long x[1000006],y[1000006];
long long sum[1000006];
long long cnt[1000006];
long long check(long long k){
    memset(sum,0,sizeof(sum)*2);
    for(long long i=1;i<=n;i++){
        sum[i]=sum[i-1],cnt[i]=cnt[i-1];
        if(w[i]>=k) sum[i]+=v[i],cnt[i]+=1;
    }
    //for(long long i=1;i<=n;i++){
        //cout<<sum[i]<<" ";
    //}
    long long num=0;
    for(long long i=1;i<=m;i++){
        num+=(cnt[y[i]]-cnt[x[i]-1])*(sum[y[i]]-sum[x[i]-1]);
        //cout<<num<<endl;
    }
    return num;
}
int main(){
    n=rd(),m=rd(),s=rd();
    long long l=0x7ffffffffffff,r=0;
    for(long long i=1;i<=n;i++){
        w[i]=rd(),v[i]=rd();
        r=max(w[i],r),l=min(l,w[i]);
    }
    for(long long i=1;i<=m;i++) x[i]=rd(),y[i]=rd();
    r++,l--;
    long long ans=0x7ffffffffffff;
    //write(check(4));
    while(l<=r){
        long long mid=(l+r)>>1;
        long long h=check(mid);
        if(abs(h-s)<ans) ans=abs(h-s);
        if(h>s) l=mid+1;
        else r=mid-1;
    }
    write(ans);
    return 0;
}

NOIP2011聰明的質監員