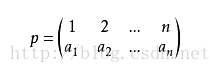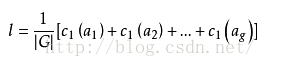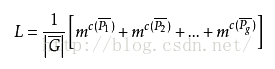置換群也是群論當中一個比較重要的內容，可是在離散課上老師直接跳過了這章內容我也是……(日了dog了)，自己看了半天資料總算是有點眉目了。

1.置換群：

首先我們來介紹一下置換，設S為一個n個元素的集合，置換就是S->S的一個雙射函式。寫出來看起來就像是給這n個元素換位置一樣

我們一般的寫法為：

有時候我們會看到一些置換的寫法是這樣的(……)(……)……，一開始小編看著也是一臉懵逼，不知道是什麼意思，後來才知道一個括號裡面的就是一個迴圈節。

舉個例子，給出一排排列數，6,3,4,2,1,5，最終要把它變成1,2,3,4,5,6，我們在變換的時候可以發現其實是有一些迴圈節的，比如，我們移動6，就可以得到6->5->1->6，這就是一個迴圈節，當然3->4->2->3也是一個迴圈節，我們就可以把這個置換寫為(6,5,1)(3,4,2)這種乘積的形式。

我們把S上的所有的置換組成的集合，關於置換乘積(就是雙射函式的複合運算)所構成的群稱之為n元對稱群，而n元對稱群的任何子群稱之為n元置換群，這就是關於我們置換群的概念問題了。

2.burnside引理：

接下來小編講一下burnside引理，首先還是從概念上講起。在一個置換群G={a1,a2,a3……ak}中，把每個置換都寫成不相交迴圈的乘積。 設C1(ak)是在置換ak的作用下不動點的個數，也就是長度為1的迴圈的個數。通過上述置換的變換操作後可以相等的元素屬於同一個等價類

那麼等價類的個數就等於：

關於這個引理的證明，比較複雜，大家有興趣的可以在百度百科上看(好吧，小編承認自己解釋不清楚)，

舉一個burnside引理解決問題的一個例子：一正方形分成4格，2著色，有多少種方案？其中，經過轉動相同的圖象算同一方案。

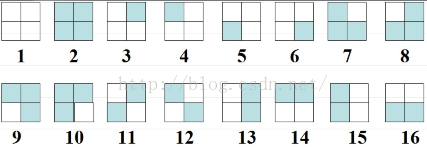
顯然，從填色的角度講，一共有2^4=16種填色情況：

關於轉動，一共有四種置換方法，我們分別列出來

不動(360度)：a1=(1)(2)…(16)
逆時針轉90度 ：a2=(1)(2)(3 4 5 6)(7 8 9 10) (11 12)(13 14 15 16)
順時針轉90度 ：a3=(1)(2)(6 5 4 3)(10 9 8 7)(11 12)(16 15 14 13)
轉180度：a4=(1)(2)(3 5)(4 6)(7 9)(8 10)(11)(12) (13 15)(14 16)
由Burnside引理，共有(16+2+2+4)/4=6(種方案)

不知道大家看懂了沒有，Burnside引理可以針對影象集的轉動群來求解，但是當多種顏色著色的時候，理論上還是可以用到Burnside引理(這句話摘的別人的，但是小編其實並不知道怎麼搞)，一般還是用到Pólya定裡來求解。

3.Pólya定理：

在一個置換群G={a1,a2,a3……ak}中，設C(ak)是在置換ak的迴圈節個數，那麼用m種顏色染圖這n個物件，則不同的染色方案數為：

證明小編依然還是不做過多說明，簡單的解釋一下這個C(ak)，在前面小編也介紹了迴圈節的概念，那麼C(ak)就是我們的迴圈節數，也就是能構成的括號的個數，Pólya定理在計算多種顏色著色的問題的時候也是用到了很多。