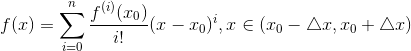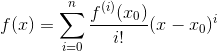淺顯易懂——泰勒展開式
阿新 • • 發佈:2018-12-23
第一次見到泰勒展開式的時候,我是崩潰的。泰勒公式長這樣:
好奇泰勒是怎麼想出來的,我想,得儘量還原公式發明的過程才能很好的理解它。
首先得問一個問題:泰勒當年為什麼要發明這條公式?
因為當時數學界對簡單函式的研究和應用已經趨於成熟,而複雜函式,比如: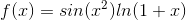
讓我們沿著泰勒同學(假裝泰勒是這麼想的)的思路來:
要讓一個複雜函式變簡單,能不能把它轉換成別的表示式?比如函式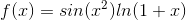
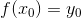 。暫時看不出有什麼規律。
。暫時看不出有什麼規律。
那就繼續增大研究的物件,比如說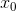
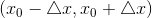
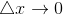
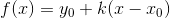
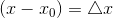
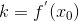
因為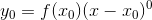
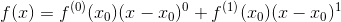
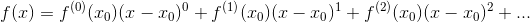
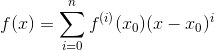
先求個導試試: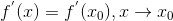
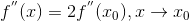
我們可以嘗試把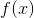
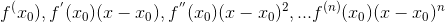
讓我們對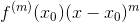
一階導: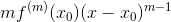
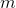
二階導: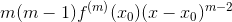
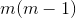
......
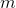
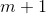
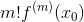
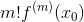
這裡規律很明顯了,
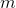 階導以前呢?還是蠻複雜的,不過不用擔心,因為
階導以前呢?還是蠻複雜的,不過不用擔心,因為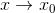 ,即
,即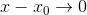 ,所以
,所以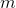 階導以前也都是0,而
階導以前也都是0,而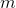 階導就是
階導就是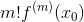 。perfect!
。perfect!
這樣就很清晰了:對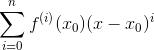
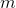
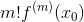
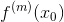
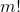
即乘於一個