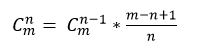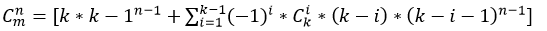題意:n朵花,從m種顏色中選擇k種顏色使得相鄰花不同色的方案數.

對於比較小的資料,這道計數題可以用DP做,DP[i][j]表示染i朵花用了j種顏色的方案數,那麼對於後i-1朵花,要麼用了j種顏色,要麼用了j-1種顏色,轉移方程也就很簡單了DP[i][j] = j*(DP[i-1][j-1]+DP[i-1][j]).

但是這題的資料比較大,所以考慮容斥原理.

首先組合數遞推公式:

顯然要先把1-1e6的逆元求出來.

考慮k種顏色塗色時相鄰不同色的方案有k*(k-1)^(n-1),這之中含有實際只用了1種顏色,2種顏色....k-1種顏色,需要把他們減去.

所以減去1種顏色沒有用的情況,但是這裡麵包含了2種顏色沒有用的情況,所以要加上2中顏色沒有用的情況....這麼迭代下去就是容斥,把多的減掉少的加上.

式子就是:

有個學長說我每次寫程式碼都自帶大常數,果不其然,這一份挫到卡卡過=.=

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <time.h>
#include <cmath>
using namespace std;
#define mod 1000000007
#define maxn 1111111

long long f[maxn];//逆元
void init(){
    f[1] = 1;
    for (int i = 2; i <= 1000000; i++){
        f[i] = (long long)(mod - mod/i) * f[mod % i] % mod;
    }
}

long long n, k, m;
long long c[maxn];

long long qpow (long long a, long long b) {
    a %= mod;
    if (b == 0)
        return 1;
    long long ans = qpow (a, b>>1);
    ans = ans*ans%mod;
    if (b&1)
        ans = ans*a%mod;
    return ans;
}

int main () {
    init ();
    int t, kase = 0;
    scanf ("%d", &t);
    while (t--) {
        scanf ("%lld%lld%lld", &n, &m, &k);
        printf ("Case #%d: ", ++kase);
        if (k == 1 && n == 1) {
            printf ("%lld\n", m);
            continue;
        }
        if (k == 1 && n > 1) {
            printf ("0\n");
            continue;
        }
        long long ans = m%mod;
        for (long long i = 2; i <= k; i++) {
            ans = ans*(m-i+1)%mod*f[i]%mod;
        }
        c[1] = k%mod;
        for (long long i = 2; i <= k; i++) {
            c[i] = c[i-1]*(k-i+1)%mod*f[i]%mod;
        }
        long long res = k*qpow (k-1, n-1) % mod; 
        for (long long i = 1; i < k; i++) {
            long long id = ((i&1) ? -1 : 1);
            long long cur = c[i]*(k-i)%mod*qpow (k-i-1, n-1)%mod;
            cur *= id;
            if (cur < 0)
                cur += mod;
            res += cur;
            res %= mod;
        }
        printf ("%lld\n", ans*res%mod);
    }
    return 0;
}