一、函式極限的概念

函式極限的引入

數列{xn}:xn = f(n)

lim n->∞ xn=a : 當自變數n取正數而無限增大時,f(n)無限接近於確定的數a

函式的極限:在自變數的某個變化過程中，如果對應的函式值無限接近於某個確定的數，那麼這個確定的數就叫做在一變化古城中的函式的極限

自變數變化的兩種情況:

1.自變數x任意地接近於有限值x0(記作x->x0) 對應地函式值f(x)地變化情形

2.自變數x地絕對值|x|無限增大(記作x->∞) 對應地函式值f(x)的變化情形

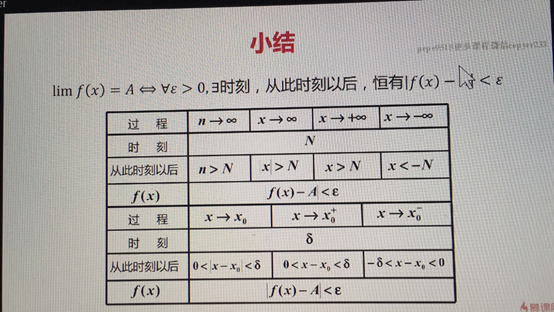
自變數變化的過程:x->x0 f(x)->A 稱A是f(x)當x->x0時的極限

f(x)無限接近於A

|f(x)-A|可以任意小

|f(x)-A|>

x無限接近於0

x->x0

0<|x-x0|<

是某個正數 是以 為半徑 x0點的去心鄰域

自變數趨於有限值時函式的極限

如果對於任意給定的正數 (不論他多麼小

·總存在正數  使得對於適合不等式0<|x-x0|< 的一切x,

·所對應的函式值f(x)都滿足不等式|f(x)-A|<

·那麼常數A就叫做函式f(x)當x->x0時的極限

記作 f(x) = A  或f(x)->A(當x->x0) 

注意

·注1:函式極限與f(x)在x0是否有定義無關

·注2: 與任意給定的正數

·注3:找到一個 ，它體現了x接近x0的程度

二、函式極限例題與單側極限

單側極限

定理: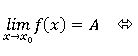   

ó f(x0+0) = f(x0-0) =A

左右極限存在但是不相等 函式極限不存在

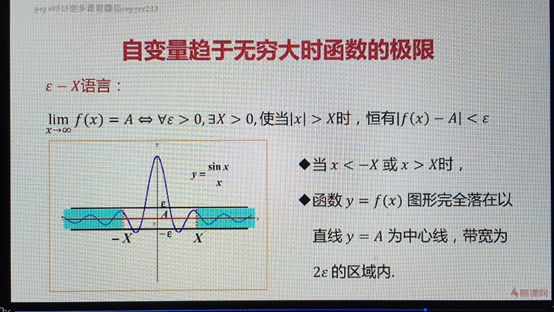
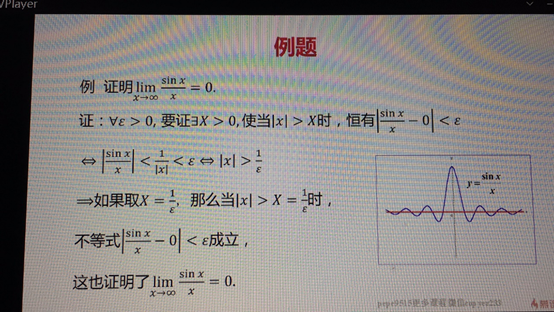
自變數趨於無窮大時函式的極限

·如果對於任意給定的正數  (不論他多麼小)

·總存在著正數X 使得對於適合不等式|x|>X的一切x

·所對應的函式值f(x)都滿足不等式|f(x)-A|<

·那麼常熟A就叫做f(x)當x->∞的極限

記作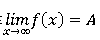  

或f(x)->A(當x->∞)

三、函式極限 的性質

1.唯一性

定理:如果limx->x0f(x)存在 那麼此極限唯一

2.區域性有界性

如果limx-x0 f(x) = A那麼存在常熟M>0和δ>0 使得當

0<|x-x0|<δ時,有|f(x)|<=M

3.區域性保號性

定理:如果lim x->x0 f(x) = A 且A>0(或A<0) 那麼存在常數δ>0 使得當0<|x-x0|<δ時 有f(x)>0(或f(x)<0)

4.函式極限與數列極限的關係

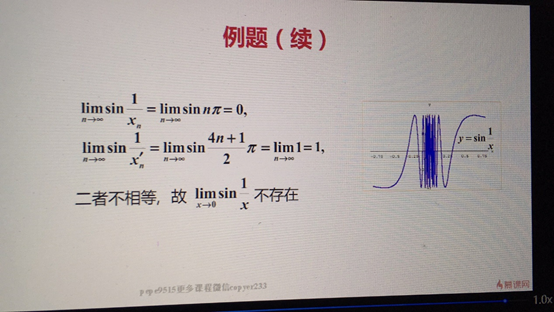
定理:如果limx->x0 f(x)存在,{xn}為函式f(x)的定義域內任一收斂於x0的數列 且滿足xn≠x0 那麼響應的函式值數列{f(xn)}必收斂,且limn->∞f(xn) = lim x->x0 f(x)

2.區域性有界性

如果limx-x0 f(x) = A那麼存在常熟M>0和δ>0 使得當

0<|x-x0|<δ時,有|f(x)|<=M

3.區域性保號性

定理:如果lim x->x0 f(x) = A 且A>0(或A<0) 那麼存在常數δ>0 使得當0<|x-x0|<δ時 有

四、小結