關於奈奎斯特穩定判據應用中的理解
根據上一篇文章,我們知道要想判定系統穩定性,只需要找到當 S繞奈奎斯特路徑一圈後, G(s)H(s)所經過的路徑繞 (−1,j0)的次數就可以了,現在我們就來深入探討當 S繞奈奎斯特路徑一圈後, G(s)H(s)的路徑到底是什麼樣,
接下來我們分為兩種情況討論
1. G(s)H(s)在虛軸上無極點

函式在虛軸上時的情況很簡單,我們不予討論,我們主要討論一下,函式在大圓弧上的情況。
設
S=R→∞limRe−jϕ它在GH平面上的對映為
G(s)H(s)∣s=R→∞limRe−jϕ=(R→∞limanbm⋅Rn−m1)ej(n−m)ϕ
(推導過程自己弄)
當n = m 時
G(s)H(s)∣s=R→∞limRe−jϕ=anbm=K
即圓弧對映為常數K
當
n>m時,
G(s)H(s)∣s=R→∞limRe−jϕ=0
即圓弧對映為原點
2. G(s)H(s)在虛軸上有極點
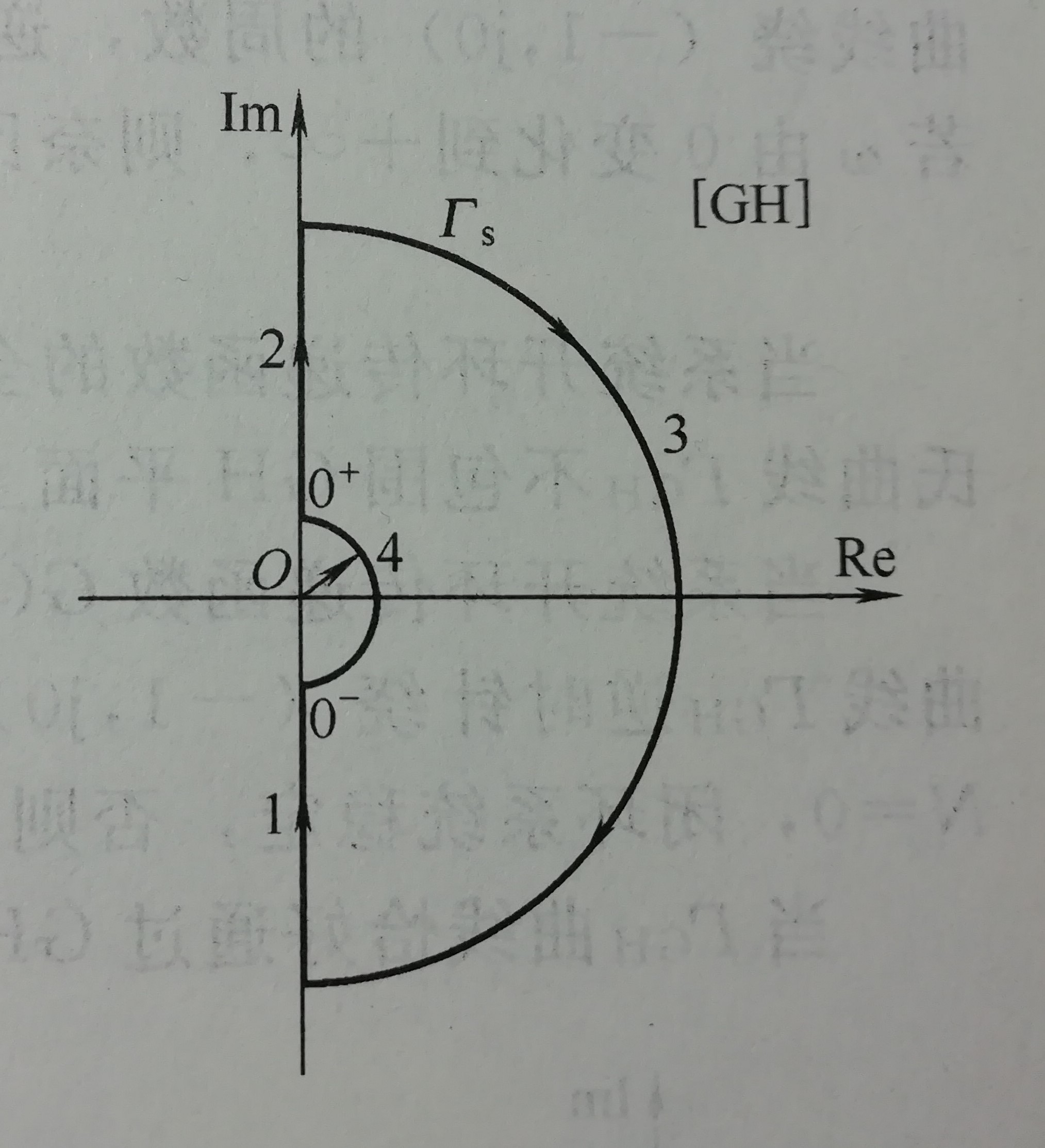
我們現在只關注那個小圓弧即
s=R→0limRejθ(−2π⩽−2π),
設系統開環傳遞函式為
G(s)H(s)=sν(s−p1)(s−p2)…(s−pm)k(s−z1)(s−z2)…(s−zm)
ν稱為系統型別,經過推導可以得到
G(s)H(s)∣s=r→0limrejθ=r→0limrνKe−jνθ
上式表明,當 s在小圓弧上逆時針變化時 G(s)H(s)的變化軌跡是一個順時針的無窮大的圓弧,弧度為 νπ
相關推薦
關於奈奎斯特穩定判據應用中的理解
根據上一篇文章,我們知道要想判定系統穩定性,只需要找到當 S S S繞奈奎斯特路徑一圈後,
對奈奎斯特穩定判據的理解
對奈奎斯特穩定判據的理解 設系統的開環傳遞函式為 G ( s
奈奎斯特定理 and 香農定理
存在 1的個數 就是 數據 IT sha 概念 idt 次數 -----------------------整理自<21ic電子網> 奈奎斯特定理(Nyquist‘s Theorem)和香農定理(Shannon‘s Theorem)是網絡傳輸中的兩個基本定理;要
奈奎斯特
首先要記住一個準則,即奈奎斯特准則: 數字基帶傳輸系統無碼間干擾的充要條件是傳輸通道的總的頻域波形為 sum{ H(f-k/Ts)}=常數. 這樣的話,就可以
解讀夏農定理、奈奎斯特定理、編碼與調製
https://mp.weixin.qq.com/s?__biz=MjM5ODYyODM4Mg==&mid=2655684738&idx=1&sn=70a65dfe4f397d4335476ed8e3d9ddba&chksm=bd79f5f38a0e7ce5f
奈奎斯特准則與夏農定理
資訊學中的概念繁多,且與日常生活中的概念多有混淆,自己在學習相關知識的時候感覺很亂,在此做一個小結。 一 定義 1.頻寬:模擬通道的頻寬 *W=f2-f1* 其中f1是通道能夠通過的最低頻率,f2是通道能夠通過的最高頻率,兩者都是由通道的物理特性決定的。數字通
奈奎斯特三大準則
夏農定理描述了有限頻寬、有隨機熱噪聲通道的最大傳輸速率與通道頻寬、訊號噪聲功率比之間的關係.在有隨機熱噪聲的通道上傳輸資料訊號時,資料傳輸率Rmax與通道頻寬B,信噪比S/N關係為: Rmax=B*log2(1+S/N)。注意這裡的log2是以2為底的對數,下同。在訊號處理和資訊理論的相關領域中,通
理解奈奎斯特定理和夏農定理
轉自: http://blog.ednchina.com/tengjingshu/179701/message.aspx ―――――――――――――――――――――――――――――――――― ――――― 奈奎斯特定理(Nyquist's Theorem)和夏農定理(Sh
奈奎斯特采樣定理
公式 png mage 開始 http img 嚴格 因此 linx 采樣定理1928年由美國電信工程師H.奈奎斯特首先提出來的,因此稱為奈奎斯特采樣定理。 1933年由蘇聯工程師科捷利尼科夫首次用公式嚴格地表述這一定理,因此在蘇聯文獻中稱為科捷利尼科夫采樣定理。
Routh-Hurwitz Criterion 勞斯穩定判據
處理方法 函數 -m 要求 case 運用 進行 滿足 不同 Routh-Hurwitz Criterion 為什麽僅僅要有一個極點在右半平面,那麽系統就不會穩定? 比如H(s) =( 1/(s+1) ) * ( 1/(
演算法-----勞斯-赫爾維茨(Routh-Hurwitz)穩定判據(轉)
判別系統穩定性最基本的方法是根據特徵方程式的根的性質來判定。但求解高於三階的特徵方程式相當複雜和困難。所以在實際應用中提出了各種工程方法,它們無需求特徵根,但都說明了特徵根在複平面上的分佈情況,從而判別系統的穩定性。本節主要介紹代數判據。 (一) 系統穩定性的初步判別 設已知控制系統的特徵方程 式中所有係
斯特靈公式的應用
斯特靈公式的多種應用 斯特靈公式是一條用來去n階乘近似解的數學公式,可以用來估算某數的大小,結合log可以估算某數的位數,或者估算某數的階乘是另一個數的倍數 #include<iostream> #include<cmath> usin
Routh-Wurwitz 穩定判據
Routh-Hurwitz 穩定判據 系統穩定性概念 A stable system should exhibit a bounded output if the corresponding input is bounded. The closed
勞斯判據的證明及應用
本文在word上編輯後貼上而來,本文中提及的勞斯判據證明方法不是從赫爾維茨判據而來,而是依據參考文獻1做出的證明,其中與國內教材不同的勞斯表也已做出證明。 補充:後來又做了這個系統的超前滯後校正,貼
數據結構 - 單源最短路徑之迪傑斯特拉(Dijkstra)算法詳解(Java)
previous 代碼 map class matrix () count 就是 可能 給出一個圖,求某個端點(goal)到其余端點或者某個端點的最短路徑,最容易想到的求法是利用DFS,假設求起點到某個端點走過的平均路徑為n條,每個端點的平均鄰接端點為m,那求出這個最短
[數據結構]迪傑斯特拉(Dijkstra)算法
graph tegra src img exe 經歷 mage length arraylist 基本思想 通過Dijkstra計算圖G中的最短路徑時,需要指定起點vs(即從頂點vs開始計算)。 此外,引進兩個集合S和U。S的作用是記錄已求出最短路徑
斯特林數應用
n) begin mes n! 一行 spl 函數 未知數 display 基礎定義不再說明。請先學完數學基礎I~IV、多項式基礎I~II、生成函數、組合基礎I~II再來看這篇。 排列到循環 \[n!=\begin{bmatrix}n\\ [1,n]\end{bmatrix
hdu1018--斯特靈公式
math ++ namespace class cin 3.1 open brief http 斯特靈公式 Wiki http://zh.wikipedia.org/wiki/斯特林公式 /** \brief hdu 1018 * * \param date 2
為什麽邏輯斯特回歸(logistic regression)是線性模型
softmax bsp 之間 ima 打破 regress 什麽 影響 線性變換 一個典型的logistic regression模型是: 這裏明明用了非線性函數,那為什麽logistic regression還是線性模型呢? 首先,這個函數不是f(y,x)=0的函數
Gym Gym 101147G 第二類斯特林數
event for cnblogs color ide hide col problem pan 題目鏈接:http://codeforces.com/gym/101147/problem/G 題意:n個人,去參加k個遊戲,k個遊戲必須非空,有多少種放法? 分析: 第二
