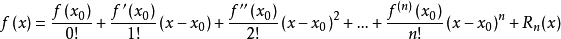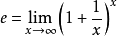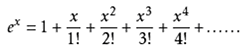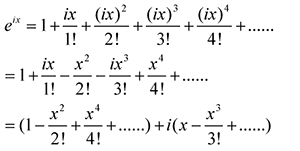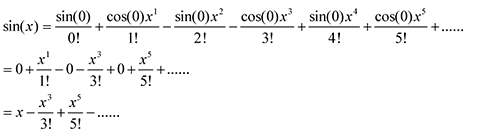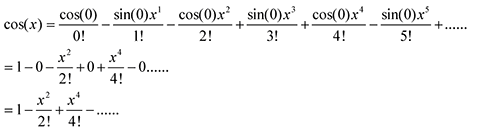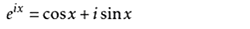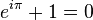最完美的公式——尤拉公式
1. 引子
看傅立葉變換的時候,一直奇怪,冪指數是怎麼對映成三角函式的?學習了一下尤拉公式,果然很神奇,用到了自然常數e,圓周率π,虛數i,三角函式sin/cos,指數,還有泰勒展開.倒不是演算法有多難,只是涉及基礎太多,經常被卡住,總結如下.
2. 泰勒展開
泰勒展開是用多項式逼近原函式,這麼做是因為像sin(x)這樣的函式,如果代入x=4很難算出結果,但是將x的值代入形如f(x)=a0+a1x+a2x^2+a3x^3…的多項式就很容易計算。具體是用原函式的導數實現的,把函式展開成多項式,公式如下:
其中Rn(x)是餘項
3. 自然常數e
e是自然常數(尤拉數),它是一個約等於2.718的無理數,定義是
它的含義可以通過複利來理解,假設你有1塊錢,年利息是1塊錢(100%),一年後可拿到兩塊錢(1+1/1)^1=2;按利滾利計算,如果半年付一次利息(1+1/2)^2=2.25;一個月付一次息,(1+1/12)^12=2.61;每天付一次息,(1+1/365)^365=2.715,當x驅於無窮時e約為2.718.
4. 自然指數e^x的泰勒級數展開
把e^x在x=0處展開,由於e^0=1且e^x的導數還是e^x,展開後得到
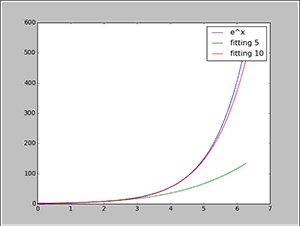
上圖是e^x,以及展開式前5項和前10項擬合的影象
5. 複數
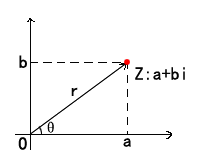
複數是形如a+b*i的數,其中a,b是實數,i^2=-1.(對應直角座標系)
在複變函式(複數作為自變數和因變數的函式)中,變數z可以寫成z=r (cosθ+ isinθ) .r是z的模,即r = |z|; θ是z的輻角,複數記作點Z(a,b)或向量OZ(對應極座標系)
把乘一次i看成相對0點逆時針轉90度,乘兩次,轉180度,轉成實軸的-1,轉三次是-i,轉四次又回到單位1。因此可以把其虛部看成定義如何旋轉。
6. 把虛數i代入e^x的展開式
虛數i是-1開方,因此有i^1=i, i^2=-1,i^3=-i,i^4=1
此時可以看到其結果分為實部和虛部兩部分
7. 把sin(x)做泰勒級數展開
在x=0處展開,由於sin(0)=0,cos(0)=1,sin’(x)=cos(x),cos’(x)=-sin(x)
8. 把cos(x)做泰勒級數展開
在x=0處展開
9. 尤拉公式
由以上幾步,可以看到e^ix的實部和虛部正好對應sin(x)和cos(x)的展開,據此,得到尤拉公式:
尤拉公式將指數函式的定義域擴大到了複數域,建立了三角函式和指數函式的關係,被譽為“數學中的天橋”。
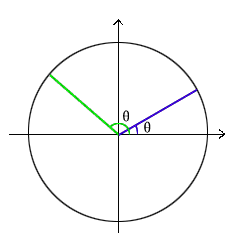
下圖中,將上式右側表示為二維座標中的點,xy軸分別表示其實部虛部,θ為轉角(即上式中的x),轉動半徑為單位1(模不變).它的幾何意義就是隨著虛部x的增加不斷轉圈.
可以把 e^(i*x) 看作通過單位圓的圓周運動來描述單位圓上的點,e^(i*x)表示在單位圓上轉動了x弧度(即某個角度時)得到的向量,以此類推,e^(πi)在單位圓上轉了半圈。顯然得到的是實軸上的-1,然後與1合併可抵消得到0 ,由此得到 :
10. 擴充套件成時間的函式
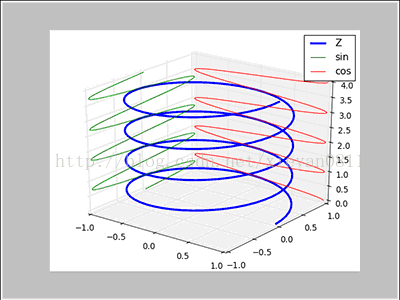
上圖中又加入了t,把e^(ix)想成e^(iwt),t是時間,w是係數。
把平面上的轉圈擴充套件成了空間中的轉圈,縱軸表示時間t,兩個橫軸分別為實部(cos(t))和虛部(sin(t)),藍線經過的點是e^ix,即,把時域上的e^ix分別投射到了實軸cos(t)和虛軸sin(t),它們都是時間t的函式.圖中可看到正餘和餘弦的投射(紅/綠),如果用python做3D圖,拖動旋轉角度效果更直觀.這就傅立葉變換原理:將時域值拆分對映到頻域,通過三角函式的疊加表示。
轉載原地址:https://blog.csdn.net/xieyan0811/article/details/72833722