尤拉公式
尤拉公式表示式
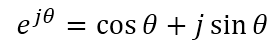
尤拉公式的幾何意
cosθ + j sinθ 是個複數,實數部分也就是實部為 cosθ ,虛數部分也就是虛部為 j
根據尤拉公式和這個點可以用 復指數 ![]() 表示,如圖:
表示,如圖:
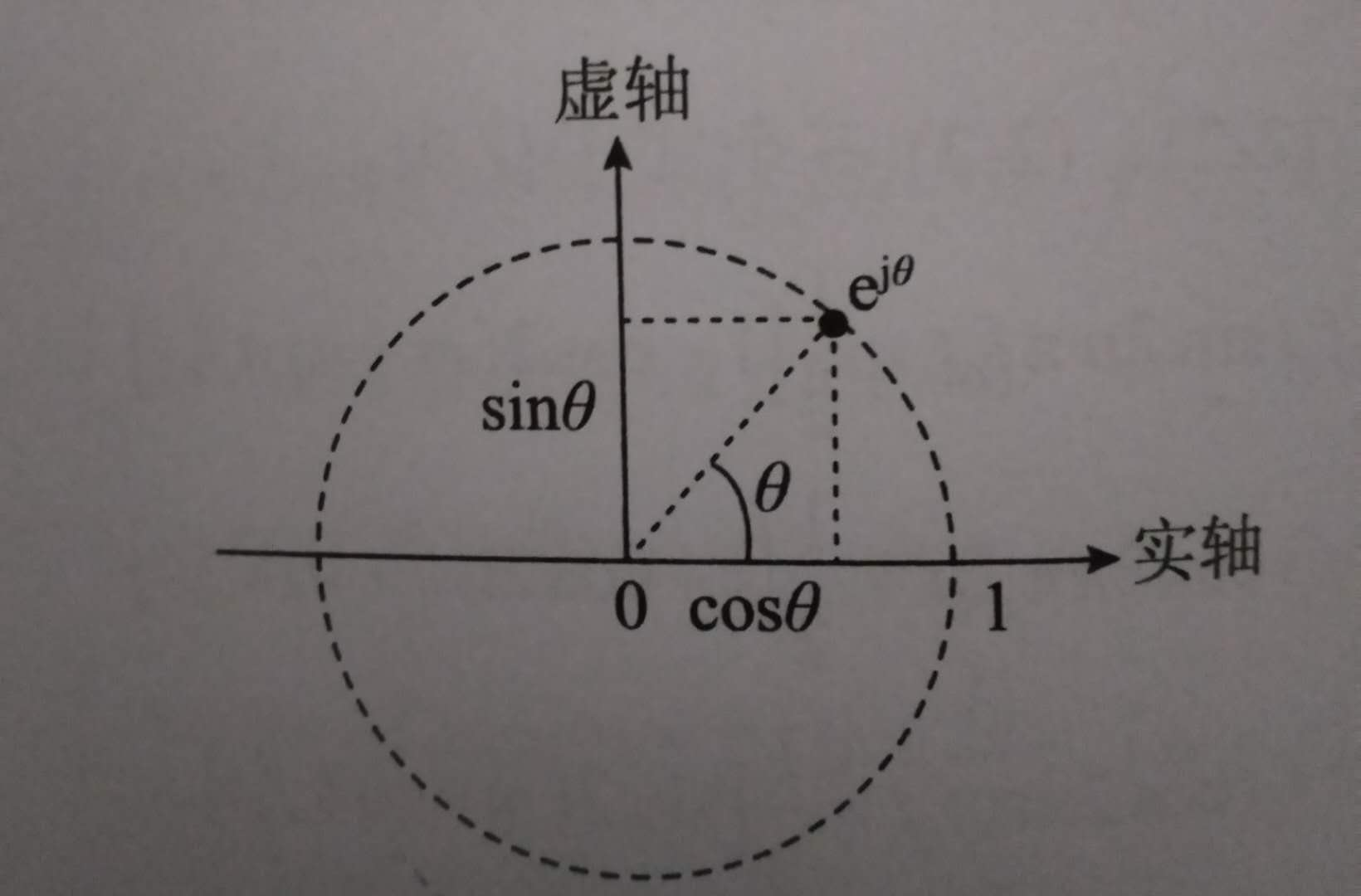
復指數 ![]() 對應的單位向量:起始端為原點,模長為1,輻角為 θ。
對應的單位向量:起始端為原點,模長為1,輻角為 θ。
複數 z 與復指數![]() 相乘可以用向量旋轉來理解。
相乘可以用向量旋轉來理解。
![]()
![]()
表示 z 逆時針轉動 θ,如果 θ 實際是個小於0的值,那 z 就順時針轉動 θ。
用泰勒級數展開式證明尤拉公式
![]()
![]()
![]()
相關推薦
Fence Building(尤拉公式+盧卡斯)
使用尤拉公式推導,平面內的區域個數=平面內的點數+平面內的邊數+2,因為這個是在圓上,所以圓外補集的那1個區域要減去, 1.所以最後+1而不是+2。 點數=C(n,4),即每4個點連線就有一個平面內的點產生 .邊數=C(n,2),即每兩個點連線就產生一條邊。 這題的範圍
最完美的公式——尤拉公式
1. 引子 看傅立葉變換的時候,一直奇怪,冪指數是怎麼對映成三角函式的?學習了一下尤拉公式,果然很神奇,用到了自然常數e,圓周率π,虛數i,三角函式sin/cos,指數,還有泰勒展開.倒不是演算法有多難,只是涉及基礎太多,經常被卡住,總結如下. 2. &nbs
[HDU 5728] PowMod (尤拉函式的積性+尤拉公式降冪+尤拉篩)
HDU - 5728 求 K=∑i=1mϕ(i∗n)mod1000000007 其中 n是 square-free number 求 ans=KKKK..modp 先求 K 由於 ϕ(n)是積性函式,所以對於 n的每個素因子可以提出
世界上最完美的公式 ----尤拉公式
尤拉公式 在數學歷史上有很多公式都是尤拉(leonhard euler 公元1707-1783年)發現的,它們都叫做 尤拉公式,它們分散在各個數學分支之中。 (1)分式裡的尤拉公式: a^r/(a-b)(a-c)+b^r/(b-c)(b-a)+c^r
Codeforces 933 C. A Colourful Prospect (平面圖,尤拉公式)
Description Firecrackers scare Nian the monster, but they’re wayyyyy too noisy! Maybe fireworks m
關於尤拉公式在ACM中的應用
題目描述:你有一塊橢圓的地,你可以在邊界上選n個點,並兩兩連線得到n(n-1)/2條線段。他們最多能把土地分成多少個部分? 輸入:輸入包含多組測試資料,每組測試資料佔一行,代表在橢圓邊界選擇點的數量n(n>=2)
最美的公式之一— —尤拉公式
ei∗π+1=0 尤拉公式將數學中最基本的e,i,π聚在一起,同時加入了數學也是哲學中最重要的0與1,再以簡單的加號相連。該公式的巧妙簡潔讓人頓感自然的美妙。 不同領域的人看到尤拉公式就會產生不同的幻想。比如,機械領域的人就看到圓周與振動運動的互相轉換,以此
如何推導尤拉公式e^iθ=cosθ+i*sinθ
相信大多數人都知道大名鼎鼎的數學最美的公式: 為什麼說它是最美的呢?因為它包含了指數裡最基本的e,複數裡最基本的 i ,圓頻率最基本的 π,以及自然數裡最基本的0和1。 本質上這個公式是由 這個公式推導過來的,把θ換成π即可。 那麼這個公式是如何得到的呢?可以使用高等
尤拉公式
開發十年,就只剩下這套架構體系了! >>>
101550E (Exponial Gym)尤拉降冪公式
題意: 給定兩個數n和m,求 。 題解: 使用尤拉定理降冪公式: 這裡引用一位大佬的公式證明:尤拉降冪公式的證明 程式碼: #include <iostream> #include
hdu 1411 校慶神祕建築 (尤拉四面體公式)
題目連結:哆啦A夢傳送門 參考部落格: https://www.cnblogs.com/dgsrz/articles/2590309.html 1,建議x,y,z直角座標系。設A、B、C少拿點的座標分別為(a1,b,1,c1),(a2,b2,c2),(a3,b3,c
UVA-11426 GCD-Extreme(II) 尤拉函式+推公式
感覺很考驗思維的一道題。。我太菜了...除了最樸素的暴力就想不出來別的了QAQ.. 主要就是以下三點: 1.g[n]=g[n-1]+b[n],b[n]表示1到n-1與n的gcd的和 2.b[n]=∑(a[i]*i) (0<i<n),a[i]表示1到n-1
數論基本定理和尤拉廣義降冪公式
一. 威爾遜定理 當p為素數時,(p-1)!= -1(mod p) 其逆定理也成立,移項得:(p-1)!+1整除p 二. 費馬小定理 當gcd(a,p)= 1且p為素數時,a ^(p-1)= 1(mod p) 而a ^ 0 = 1(mod p),因此存在長度
FZU 1759-Super A^B mod C (尤拉函式+降冪公式)
尤拉函式是指:對於一個正整數n,小於n且和n互質的正整數(包括1)的個數,記作φ(n) 。 通式:φ(x)=x*(1-1/p1)*(1-1/p2)*(1-1/p3)*(1-1/p4)…..(1-1/pn),其中p1, p2……pn為x的所有質因數,x是不為0的整數。φ(1)=1(唯一和1互質的數就是1
旋轉矩陣與尤拉角之間互換公式
/*弧度 角度 */#define PAI 3.141592653589793#define RADIAN(PAI / 180.0 ) //弧度 = 角度 * π / 180#define ANGLE (180.0 / PAI ) //角度 = 弧度 * 180
【數學】尤拉恆等式:史上最完美的數學公式,沒有之一!
萊昂哈德·尤拉是18世紀最偉大的數學家之一,也是人類歷史上最傑出的數學家之一。作為一個多產的數學家,尤拉貢獻不可估量,他提出了許多對現代數學不可或缺的概念。在尤拉的一生中,它出版了885份關於關於數學和其他學科的論文和書籍。即使是後來失明瞭,他仍然筆耕不輟。尤拉在失明之後還
尤拉降冪公式的證明
尤拉降冪公式與證明 尤拉降冪公式 AK≡AK%ϕ(m)+ϕ(m)(modm)K>ϕ(m)AK≡AK%ϕ(m)+ϕ(m)(modm)K>ϕ(m) 證明 今天在牛客多校的群裡看一個數學大佬寫的證明,不過是拍照,我決定動手自己
FZU 1759 Super A^B mod C (尤拉函式,快速冪,降冪公式)
一道嚇人的題。。 不禁再次感嘆數學真偉大,使用下面的降冪公式很簡單就寫出來了。 phi是尤拉函式,如果不太清楚尤拉函式是什麼,怎麼求尤拉函式,可以看看下面這兩個部落格,或者參考維基百科。 學會了求尤拉函式值,我們就可以利用上面那個降冪公式來計算結果了。 #in
尤拉角與旋轉矩陣之間的轉化公式及原理
1.背景說明 首先,說明幾點需要注意的問題: a.左手座標系與右手座標系:既然是在座標系中進行變換,首先就要了解座標系的類別。同樣的資料在左手座標系和右手座標系會有不同的呈現結果。所以,所有涉及到座標系的問題,不說明基於左手座標系還是右手座標系就有可能帶著小白走
莫比烏茲反演, 尤拉函式等亂七八糟的數論公式推導題
前言 最近學了些數論函式,有了一些小小小小的套路經驗 強烈推薦以下幾個部落格 數論函式變換總結 金策大佬 超詳細 課件 狄利克雷卷積 定義:(f×g)(n)=∑d|nf(d)g(nd)(f×g)(n)=∑d|nf(d)g(nd) 方

