題目描述：有3扇關閉的門，一扇門後面停著汽車，其餘門後是山羊，只有主持人知道每扇門後面是什麼。參賽者可以選擇一扇門，在開啟它之前，主持人會開啟另外一扇門，露出門後的山羊，然後允許參賽者更換自己的選擇。

1、按照你的第一感覺回答，你覺得不換選擇能有更高的機率獲得汽車，還是換選擇能有更高的機率獲得汽車？或機率沒有發生變化？

答：換選能有更高几率獲得汽車！

2、請自己認真分析一下“不換選擇能有更高的機率獲得汽車，還是換選擇能有更高的機率獲得汽車？或機率沒有發生變化？” 寫出你分析的思路和結果。

答：因為我本學期有概率論與數理統計這門課，我首先想到的是用概率知識來解決這個問題。

       可能用到的概率知識  1.全概率公式

                                         2.條件概率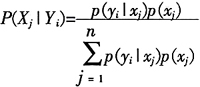               （來源於百度百科不算抄襲吧？？？）

      在預設讀者已經掌握了上述基本原理後開始解決這個問題。

      首先，參賽者有兩種選擇1.更換選擇。2.不更換選擇。

               1.更換選擇：在第一次選擇中，假設有第一種情況，參賽者很幸運的選中了車（概率為1/3），參賽者聽了主持人的蠱惑，更換了選擇，那麼他選中車的概率為1/3*0=0.

                                                         假設有第二種情況，參賽者不幸選中了羊  （概率為2/3），參賽者又聽了主持人的蠱惑，更換了選擇，那麼他選中車的概率為2/3*1=2/3（主持人打開了一扇羊門，剩下的一個門一定是車（在參賽者選中羊的條件下

                                    綜上所訴，在更換選擇的情況下，選中車的概率為0+2/3=2/3.

                2.不更換選擇：在第一次選擇中，假設有第一種情況，參賽者很幸運的選中了車（概率為1/3），參賽者沒有聽主持人的蠱惑，沒有更換選擇，那麼他選中車的概率為1/3*1=1/3.

                                                             假設有第二種情況，參賽者不幸選中了羊（概率為2/3），參賽者沒有聽主持人的蠱惑（或者說勸阻），沒有更換選擇，那麼他選中車的概率為2/3*0=0.

                                   綜上所述，在不更換選擇的情況下，選中車的概率為1/3+0=1/3。

 所以我的直覺很準。

3、請設法編寫程式驗證自己的想法，驗證的結果支援了你的分析結果，還是沒有支援你的分析結果，請寫出程式執行結果，以及其是否支援你的分析。（提示：可以藉助隨機數函式完成此程式）

驗證結果支援了我的分析結果！

 以下為python進行模擬的程式碼

from random import *
a=0
b=0
n=1000000#n1為不改選擇的次數，n2為更改選擇的次數,n為實驗次數。
for i in range(n):
    cardoornumber=randint(1,3)
    thenumberichoose=randint(1,3)
    if cardoornumber==thenumberichoose:
        a+=1
    else:
        b+=1
print('更改選擇的概率為{}'.format(a/n))
print('不更改選擇的概率為{}'.format(b/n))

以下為實驗結果概率

更改選擇的概率為0.333512   （約等於1/3）
不更改選擇的概率為0.666488（約等於2/3）

所以我的直覺真的很準！！！