免費餡餅

　　都說天上不會掉餡餅，但有一天gameboy正走在回家的小徑上，忽然天上掉下大把大把的餡餅。說來gameboy的人品實在是太好了，這餡餅別處都不掉，就掉落在他身旁的10米範圍內。餡餅如果掉在了地上當然就不能吃了，所以gameboy馬上卸下身上的揹包去接。但由於小徑兩側都不能站人，所以他只能在小徑上接。由於gameboy平時老呆在房間裡玩遊戲，雖然在遊戲中是個身手敏捷的高手，但在現實中運動神經特別遲鈍，每秒種只有在移動不超過一米的範圍內接住墜落的餡餅。現在給這條小徑如圖示上座標： 

　　為了使問題簡化，假設在接下來的一段時間裡，餡餅都掉落在0-10這11個位置。開始時gameboy站在5這個位置，因此在第一秒，他只能接到4,5,6這三個位置中其中一個位置上的餡餅。問gameboy最多可能接到多少個餡餅？（假設他的揹包可以容納無窮多個餡餅） 

Input

　　輸入資料有多組。每組資料的第一行為以正整數n(0<n<100000)，表示有n個餡餅掉在這條小徑上。在結下來的n行中，每行有兩個整數x,T(0<T<100000),表示在第T秒有一個餡餅掉在x點上。同一秒鐘在同一點上可能掉下多個餡餅。n=0時輸入結束。 
Output

　　每一組輸入資料對應一行輸出。輸出一個整數m，表示gameboy最多可能接到m個餡餅。 
提示：本題的輸入資料量比較大，建議用scanf讀入，用cin可能會超時。 

Sample Input

6
5 1
4 1
6 1
7 2
7 2
8 3
0

Sample Output

4

解題思路：
　　本題每組資料包括餡餅數量n之後n行給出每個餡餅的掉落時間與位置，有0-10共11個位置，起始在5位置，每次只能移動到周圍兩個位置，要求輸出最大接到的餡餅數量。

　　本題類似數塔問題。

　　分析樣例資料

　　

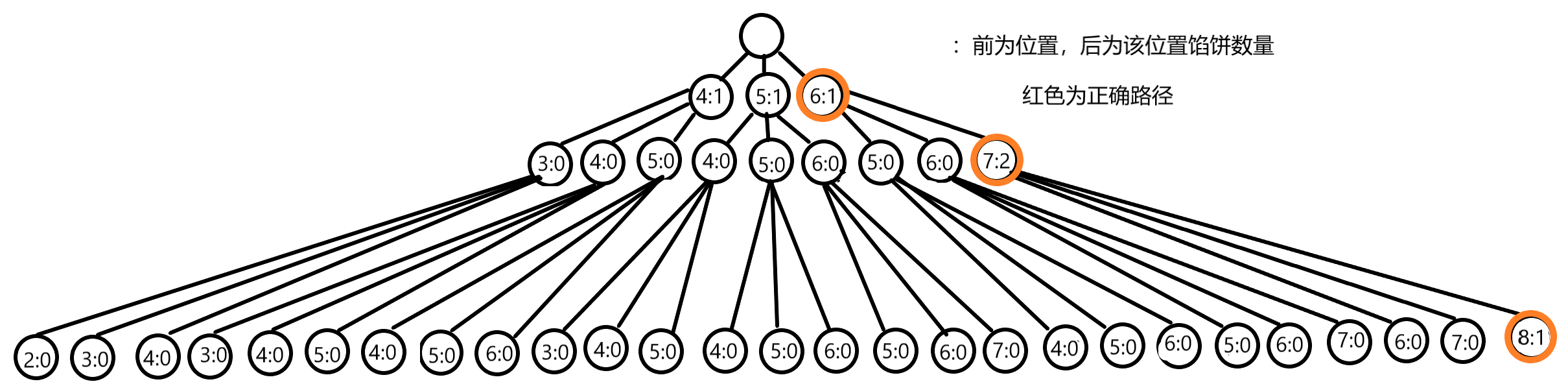
　　每個位置都可以抵達包括本身在內的3個位置我們用二維陣列dp[ i ][ j ]表示如果第 i 秒在第 j 號位置，從開始到第 i 秒最多接到多少餡餅，與數塔問題一樣都是找出一條路徑，使路徑上的權值和最大。

　　本著和數塔類似的拆解最低層的原則，該題形成的數塔的最底層為最後時間，樣例中最後一個餡餅在第3秒落下，那麼對於第三秒的某個位置j，如果第三秒gameboy剛好站在這個位置，那麼其能接到的最大餡餅數量就是第三秒該位置掉落的餡餅數量加上其第二秒所在位置的最大獲得餡餅數，而若在第三秒能抵達j位置，gameboy在第二秒一定是在j-1，j，j+1三個位置中的某一個，我們，只需要比較這三個位置的dp值並選擇最大的一個即可獲得第三秒j位置的dp值。

　　而求第二秒的三個位置的最餡餅數量又可以繼續拆分為求第一秒所對應位置的最大餡餅數量，這樣這個問題就可以被成功拆分了。

　　根據分析我們便可以寫出動態轉移方程dp[i][j] = max(max(dp[i - 1][j - 1], dp[i - 1][j]), dp[i - 1][j + 1]) + f[i][j]

　　AC程式碼

　　

 1 #include <bits/stdc++.h>
 2 using namespace std;
 3 const int maxn = 1e5+100;
 4 int dp[maxn][12];   //dp[i][j]表示如果第i秒在第j號位置，從開始到第i秒最多接到多少餡餅
 5 int f[maxn][12];    //f[i][j]的值第i秒j號位置上落下的餡餅數量
 6 int main()
 7 {
 8     int n;  //n為餡餅數量
 9     while(scanf("%d", &n) != EOF && n){
10         int maxtime = 0;
11         memset(dp, 0,sizeof(dp));
12         memset(f, 0,sizeof(f));
13         //每次運算dp與f初始化為0
14         for(int i = 0; i < n; i++){
15             int time, x;
16             scanf("%d%d", &x, &time);   //輸入每個餡餅的掉落時間與位置
17             maxtime = max(maxtime, time);   //記錄最晚掉落的餡餅時間
18             f[time][x]++;   //第time秒第x位置掉落的餡餅數量加一
19         }
20         dp[1][4] = f[1][4]; //由於第1秒接到4，5，6三個位置的其中一個位置的餡餅
21         dp[1][5] = f[1][5]; //所以若第一秒在哪個位置，第一秒最多接到的餡餅數量就是那個位置第一秒掉落的餡餅數量
22         dp[1][6] = f[1][6];
23         int ans = 0;
24         for(int i = 2; i <= maxtime; i++){  //遍歷從第二秒到最後掉落餡餅的那一秒
25             for(int j = 0; j < 11; j++){
26                 //動態轉移方程
27                 dp[i][j] = max(max(dp[i - 1][j - 1], dp[i - 1][j]), dp[i - 1][j + 1]) + f[i][j];
28                 //記錄最大值
29                 ans = max(ans, dp[i][j]);
30             }
31         }
32         printf("%d\n", ans);
33     }
34     return 0;
35 }