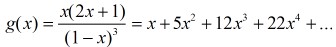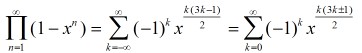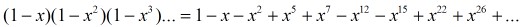DP經典 ----- 整數劃分
整數劃分 --- 一個老生長談的問題:
1) 練練組合數學能力.
2) 練練遞迴思想
3) 練練DP
總之是一道經典的不能再經典的題目:
這道好題求:
1. 將n劃分成若干正整數之和的劃分數。
2. 將n劃分成k個正整數之和的劃分數。
3. 將n劃分成最大數不超過k的劃分數。
4. 將n劃分成若干奇正整數之和的劃分數。
5. 將n劃分成若干不同整數之和的劃分數。
1.將n劃分成不大於m的劃分法:
1).若是劃分多個整數可以存在相同的:
dp[n][m]= dp[n][m-1]+ dp[n-m][m] dp[n][m]表示整數 n 的劃分中,每個數不大於 m 的劃分數。
則劃分數可以分為兩種情況:
a.劃分中每個數都小於 m,相當於每個數不大於 m- 1, 故劃分數為 dp[n][m-1].
b.劃分中有一個數為 m. 那就在 n中減去 m ,剩下的就相當於把 n-m 進行劃分, 故劃分數為 dp[n-m][m];
2).若是劃分多個不同的整數:
dp[n][m]= dp[n][m-1]+ dp[n-m][m-1] dp[n][m]表示整數 n 的劃分中,每個數不大於 m 的劃分數。
同樣劃分情況分為兩種情況:
a.劃分中每個數都小於m,相當於每個數不大於 m-1,劃分數為 dp[n][m-1].
b.劃分中有一個數為 m.在n中減去m,剩下相當對n-m進行劃分,
並且每一個數不大於m-1,故劃分數為 dp[n-m][m-1]
2.將n劃分成k個數的劃分法:
dp[n][k]= dp[n-k][k]+ dp[n-1][k-1];
方法可以分為兩類:
第一類: n 份中不包含 1 的分法,為保證每份都 >= 2,可以先拿出 k 個 1 分
到每一份,然後再把剩下的 n- k 分成 k 份即可,分法有: dp[n-k][k]
第二類: n 份中至少有一份為 1 的分法,可以先那出一個 1 作為單獨的1份,剩
下的 n- 1 再分成 k- 1 份即可,分法有:dp[n-1][k-1]
3.將n劃分成若干奇數的劃分法:(不懂)
g[i][j]:將i劃分為j個偶數
f[i][j]:將i劃分為j個奇數
g[i][j] = f[i - j][j];
f[i][j] = f[i - 1][j - 1] + g[i - j][j];
路過的大牛求解釋,謝謝~
程式碼如下所示:

/*
* hit1402.c
*
* Created on: 2011-10-11
* Author: bjfuwangzhu
*/
#include<stdio.h>
#include<string.h>
#define nmax 51
int num[nmax][nmax]; //將i劃分為不大於j的個數int num1[nmax][nmax]; //將i劃分為不大於j的不同的數int num2[nmax][nmax]; //將i劃分為j個數int f[nmax][nmax]; //將i劃分為j個奇數int g[nmax][nmax]; //將i劃分為j個偶數void init() {
int i, j;
for (i = 0; i < nmax; i++) {
num[i][0] = 0, num[0][i] = 0, num1[i][0] = 0, num1[0][i] = 0, num2[i][0] =
0, num2[0][i] = 0;
}
for (i = 1; i < nmax; i++) {
for (j = 1; j < nmax; j++) {
if (i < j) {
num[i][j] = num[i][i];
num1[i][j] = num1[i][i];
num2[i][j] = 0;
} else if (i == j) {
num[i][j] = num[i][j - 1] + 1;
num1[i][j] = num1[i][j - 1] + 1;
num2[i][j] = 1;
} else {
num[i][j] = num[i][j - 1] + num[i - j][j];
num1[i][j] = num1[i][j - 1] + num1[i - j][j - 1];
num2[i][j] = num2[i - 1][j - 1] + num2[i - j][j];
}
}
}
f[0][0] = 1, g[0][0] = 1;
for (i = 1; i < nmax; i++) {
for (j = 1; j <= i; j++) {
g[i][j] = f[i - j][j];
f[i][j] = f[i - 1][j - 1] + g[i - j][j];
}
}
}
int main() {
#ifndef ONLINE_JUDGE
freopen("data.in", "r", stdin);
#endif
int n, k, i, res0, res1, res2, res3, res4;
init();
while (~scanf("%d %d", &n, &k)) {
res0 = num[n][n];
res1 = num2[n][k];
res2 = num[n][k];
for (i = 0, res3 = 0; i <= n; i++) {
res3 += f[n][i];
}
res4 = num1[n][n];
printf("%d\n%d\n%d\n%d\n%d\n\n", res0, res1, res2, res3, res4);
}
return 0;
}

將正整數劃分成連續的正整數之和
如15可以劃分成4種連續整數相加的形式:
15
7 8
4 5 6
1 2 3 4 5
首先考慮一般的形式,設n為被劃分的正整數,x為劃分後最小的整數,如果n有一種劃分,那麼
結果就是x,如果有兩種劃分,就是x和x x + 1, 如果有m種劃分,就是 x 、x x + 1 、 x x + 1 x + 2 、... 、x x + 1 x + 2 ... x + m - 1
將每一個結果相加得到一個公式(i * x + i * (i - 1) / 2) = n,i為當前劃分後相加的正整數個數。
滿足條件的劃分就是使x為正整數的所有情況。
如上例,當i = 1時,即劃分成一個正整數時,x = 15, 當i = 2時, x = 7。
當x = 3時,x = 4, 當x = 4時,4/9,不是正整數,因此,15不可能劃分成4個正整數相加。
當x = 5時,x = 1。
這裡還有一個問題,這個i的最大值是多少?不過有一點可以肯定,它一定比n小。我們可以做一個假設,
假設n可以拆成最小值為1的劃分,如上例中的1 2 3 4 5。這是n的最大數目的劃分。如果不滿足這個假設,
那麼 i 一定比這個劃分中的正整數個數小。因此可以得到這樣一個公式i * (i + 1) / 2 <= n,即當i滿足
這個公式時n才可能被劃分。
程式碼如下:

void split(int n) {
int i, j, te, x, xlen;
for (i = 1, xlen = 0; (te = i * (i - 1) / 2) < n; i++) {
x = n - te;
if (x % i == 0) {
x /= i;
printf("%d", x);
for (j = 1; j < i; j++) {
printf("%d ", x + j);
}
printf("\n");
xlen++;
}
}
printf("%d\n", xlen);
}

以下是轉載的:
求劃分因子乘積最大的一個劃分及此乘積
問題簡述:給定一個正整數n, 則在n所有的劃分中, 求因子乘積最大的一個劃分及此乘積。例如:8 = {8}, {7, 1}, {6, 2}, {5, 3}, {4, 4}, {3, 3, 2}, {2, 2, 2, 2} 等,那麼在這些當中,3 * 3 * 2 的乘積最大,所以輸出整個劃分
和這個乘積 18。
演算法分析:這是我在某個論壇上看到的問題,以及別人針對此問題的數學分析,現簡單的整理如下:
(1)對於任意大於等於4的正整數m, 存在一個劃分m = m1+m2, 使 m1*m2 >= m證: 令m1 = int(m/2), 則 m1 >= 2 , m2 = m-m1; 那麼m2 > 2,並且 m2 >= m/2 >= m1; m1*m2 >= 2*m2 >= m; 證畢;
該證明簡單的來說就是:對於一個大於等於4的正整數m,存在一個2塊劃分的因子,這兩個因子的乘積總是不小於原數m本身。
(2)由(1)知此數最終可以分解為 2^r * 3^s。現證明 r <= 2;
證:若r > 2, 則至少有3個因子為2, 而2*2*2 < 3*3;
所以可以將3個為2的因子,換為兩個因子3;積更大;證畢。
綜合(1),(2),則有:任何大於4的因子都可以有更好的分解, 而4可以分解為2*2。
所以:此數應該分解為 2^k1 * 3^k2。而且可以證明 k1>=0 並且 k1 <= 2,因此:
A.當n = 3*r 時, 分解為 3^r
B.當n = 3*r+1時, 分解為 3^(r-1)*2*2
C.當n = 3*r+2時, 分解為 3^r*2
剩下程式設計處理,那就是太簡單了,首先是處理 <= 4的特殊情況,再對>4的情況進行模3的3種情況的判斷,最後一一輸出。可見,數學在整數劃分問題上有太強的功能。誰叫這個問題叫整數劃分呢,不與數學密切才怪! ^_^。
小學六年級奧數---整數劃分(有用結論)
例1:把14分拆成若干個自然數的和,再求出這些數的積,要使得到的積最大,應該把14如何分拆?這個最大的乘積是多少?
分析與解:我們先考慮分成哪些數時乘積才能儘可能地大。
首先,分成的數中不能有1,這是顯然的。
其次,分成的數中不能有大於4的數,否則可以將這個數再分拆成2與另外一個數的和,這兩個數的乘積一定比原數大,例如7就比它分拆成的2和5的乘積小。
再次,因為4=2×2,故我們可以只考慮將數分拆成2和3。
注意到2+2+2=6,2×2×2=8;3+3=6,3×3=9,因此分成的數中若有三個2,則不如換成兩個3,換句話說,分成的數中至多隻能有兩個2,其餘都是3。根據上面的討論,我們應該把14分拆成四個3與一個2之和,即14=3+3+3+3+2,這五數的積有最大值 3×3×3×3×2=162。
將上述結論推廣為一般情形便是:
把自然數S(S>1)分拆為若干個自然數的和: S=a1+a2+…+an,則當a1,a2,…,an中至多有兩個2,其餘都是3時,其連乘積m=a1a2…an有最大值。
例2:把1993分拆成若干個互不相等的自然數的和,且使這些自然數的乘積最大,該乘積是多少?
解:由於把1993分拆成若干個互不相等的自然數的和的分法只有有限種,因而一定存在一種分法,使得這些自然數的乘積最大。
若1作因數,則顯然乘積不會最大。把1993分拆成若干個互不相等的自然數的和,因數個數越多,乘積越大。為了使因數個數儘可能地多,我們把1993分成2+3…+n直到和大於等於1993。
若和比1993大1,則因數個數至少減少1個,為了使乘積最大,應去掉最小的2,並將最後一個數(最大)加上1。
若和比1993大k(k≠1),則去掉等於k的那個數,便可使乘積最大。
所以n=63。因為2015-1993=22,所以應去掉22,把1993分成(2+3+…+21)+(23+24+…+63)
這一形式時,這些數的乘積最大,其積為 2×3×…×21×23×24×…×63。
轉自acdreamer
五邊形定理
設第n個五邊形數為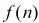
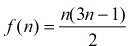
對應圖形如下:
設五邊形數的生成函式為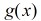
以上是五邊形數的情況。下面是關於五邊形數定理的內容:
五邊形數定理是一個由尤拉發現的數學定理,描述尤拉函式展開式的特性。尤拉函式的展開式如下:
尤拉函式展開後,有些次方項被消去,只留下次方項為1, 2, 5, 7, 12, ...的項次,留下來的次方恰為廣義五邊形數。
五邊形數和分割函式的關係
尤拉函式的倒數是分割函式的母函式,亦即:
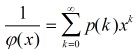
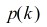
上式配合五邊形數定理,有:
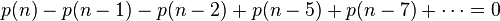
因此可得到分割函式p(n)的遞迴式:
例如n=10時,有: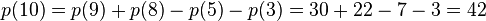
所以,通過上面遞迴式,我們可以很快速地計算n的整數劃分方案數p(n)了。
- #include <iostream>
- #include <string.h>
- #include <stdio.h>
- usingnamespace std;
- typedeflonglong LL;
- constint N=100005;
- const LL MOD=1000000007;
- LL ans[N],tmp[N];
- void Init()
- {
- int t=1000;
- for(int i=-1000;i<=1000;i++)
- tmp[i+t]=i*(3*i-1)/2;
- ans[0]=1;
- for(int i=1;i<N;i++)
- {
- ans[i]=0;
- for(int j=1;j<=i;j++)
- {
- if(tmp[j+t]<=i)
- {
- if(j&1) ans[i]+=ans[i-tmp[j+t]];
- else ans[i]-=ans[i-tmp[j+t]];
- }
- elsebreak;
- ans[i]=(ans[i]%MOD+MOD)%MOD;
- if(tmp[t-j]<=i)
- {
- if(j&1) ans[i]+=ans[i-tmp[t-j]];
- else ans[i]-=ans[i-tmp[t-j]];
- }
- elsebreak;
- }
- ans[i]=(ans[i]%MOD+MOD)%MOD;
- }
- }
- int main()
- {
- int t,n;
- Init();
- cin>>t;
- while(t--)
- {
- cin>>n;
- cout<<ans[n]<<endl;
- }
- return 0;
- }
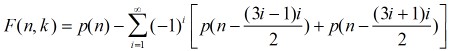
- #include <iostream>
- #include <string.h>
- #include <stdio.h>
- usingnamespace std;
- constint N = 100005;
- constint MOD = 1000000007;
- int dp[N];
- void Init()
- {
- dp[0] = 1;
- for(int i=1;i<N;i++)
- {
- dp[i] = 0;
- for(int j=1;;j++)
- {
- int t = (3*j-1)*j / 2;
- if(t > i) break;
- int tt = dp[i-t];
- if(t+j <= i) tt = (tt + dp[i-t-j])%MOD;
- if(j&1) dp[i] = (dp[i] + tt)%MOD;
- else dp[i] = (dp[i] - tt + MOD)%MOD;
- }
- }
- }
- int Work(int n,int k)
- {
- int ans = dp[n];
- for(int i=1;;i++)
- {
- int t = k*i*(3*i-1) / 2;
- if(t > n) break;
- int tt = dp[n-t];
-
相關推薦
DP經典 ----- 整數劃分
整數劃分 --- 一個老生長談的問題: 1) 練練組合數學能力. 2) 練練遞迴思想 3) 練練DP 總之是一道經典的不能再經典的題目: 這道好題求: 1. 將n劃分成若干正整數之和的劃分數。 2. 將n劃分成k個正整數之和的劃分數。 3.
【劃分型DP】整數劃分
作為劃分型DP中的基礎題,在今天也算是完成了,對DP的用法也漸漸明朗起來。 題目描述 Description 將整數n分成k份,且每份不能為空,任意兩種劃分方案不能相同(不考慮順序)。 例如
區間dp(整數劃分,石子劃分)
整數劃分(四) 基礎區間dp,程式碼: #include <cstdio> #include <cstring> long long a[20][20]; long lon
遞迴經典整數劃分問題
整數劃分問題是將一個正整數n拆成一組數連加並等於n的形式,且這組數中的最大加數不大於n。 比如6的整數劃分為 最大數(m) 6 6 5
HDU 1028 Ignatius and the Princess III(DP,整數劃分)
Ignatius and the Princess III Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others) Total Submission(s): 2
(dp)openjudge 復雜的整數劃分問題
con fin can == names 劃分數 algorithm 系列 問題 將正整數n 表示成一系列正整數之和,n=n1+n2+…+nk, 其中n1>=n2>=…>=nk>=1 ,k>=1 。正整數n 的這種表示稱為正整數n 的劃分。
51nod 1201 整數劃分 dp
bit eps 不同的 color quest stream 空間 output lac 1201 整數劃分 基準時間限制:1 秒 空間限制:131072 KB 收藏 關註 將N分為若幹個不同整數的和,有多少種不同的劃分方式,例如:
bzoj 3612: [Heoi2014]平衡【整數劃分dp】
情況 技術分享 個數 ++ const pre 全部 mage print 其實就是-n~n中求選k個不同的數,和為0的方案數 學到了新姿勢叫整數劃分,具體實現是dp 詳見:https://blog.csdn.net/Vmurder/article/details/4255
51Nod 1201 - 整數劃分(DP)
【題目描述】 【思路】 d p [ i
POJ3014 Cake Pieces and Plates【整數劃分+DP】
Cake Pieces and Plates Time Limit: 5000MS Memory Limit: 131072K Total Submissions: 6810 Accepted: 2168 Case Time Limit: 1000MS Description kcm1700, ntopi
NYOJ 90 整數劃分(遞推||dp)
整數劃分 時間限制:3000 ms | 記憶體限制:65535 KB 難度:3 描述將正整數n表示成一系列正整數之和:n=n1+n2+…+nk, 其中n1≥n2≥…≥nk≥1,k≥1。
整數劃分-劃分數(DP動態規劃)
給你一個正整數n,讓你計算出n的m劃分有幾種方法。思路:定義dp[i][j]為i的j劃分,即將i劃分為j個數字之和的方案數。1:當j<=i時,此時,劃分個數不超過i,此時是正常的劃分。 劃分的結果一定只有兩種型別:一種是j個數字,都大於0。另一種是有0,即不夠劃
NYOJ 746 整數劃分(四)區間DP
/* 區間dp,設dp[i][j] 表示在區間[0, i]之中,插入j個乘號可以得到的最大數 設a[i][j]為區間[i,j]所形成的數 所以 dp[i][j] = max(dp[k][j-1] * a[k + 1][i]) 注意數的範圍,用int不夠 */ #include <cmath>
nyoj 90 整數劃分【dp劃分數】
整數劃分 時間限制:3000 ms | 記憶體限制:65535 KB 難度:3 描述將正整數n表示成一系列正整數之和:n=n1+n2+…+nk, 其中n1≥n2≥…≥nk≥1,k≥1。 正整數n的這種表示稱為正整數n的劃分。求正整數n的不 同劃分個數。
nyoj 90 整數劃分(一) (dp||遞迴)
將正整數 n 表示成一系列正整數之和, n=n1+n2+…+nk, 其中 n1>=n2>=…>=nk>=1 , k>=1 。 正整數 n 的這種表示稱為正整數 n 的劃分。正整數 n 的不同的劃分個數稱為正整數 n 的劃分數,記作 p(n) 。 例如正整數 6 有如下 11
區間dp模型(石子歸併,括號匹配,整數劃分)
區間dp顧名思義就是在一個區間上進行的一系列動態規劃。對一些經典的區間dp總結在這裡。 1) 石子歸併問題 描述:有N堆石子排成一排,每堆石子有一定的數量。現要將N堆石子併成為一堆。合併的過程只能每次將相鄰的兩堆石子堆成一堆,每次合併花費的代價為這兩堆石子的和,經過
dp-整數劃分問題(理論分析)
原文地址:http://www.cnblogs.com/wanghetao/archive/2013/11/25/3442192.html描述 整數劃分是一個經典的問題。請寫一個程式,完成以下要求。 輸入每組輸入是兩個整數n和k。(1 <= n <= 5
nyistOJ-整數劃分(四)(區間DP)
整數劃分(四) 時間限制:1000 ms | 記憶體限制:65535 KB 難度:3 描述 暑假來了,hrdv 又要留學校在參加ACM集訓了,集訓的生活非常Happy(p
NYOJ571-整數劃分(三) | 劃分數+DP
描述 整數劃分是一個經典的問題。請寫一個程式,完成以下要求。 輸入 多組輸入資料。 每組輸入是兩個整數n和k。(1 <= n <= 50, 1 <= k <=
整數劃分問題經典解法(有用)
經典的dp! 有N多情況的整數劃分,下面就幾種這幾天學習的分別說一下: 1. 數n的劃分中,其最大值不能大於k:記其結果為f(n, k),那麼, 狀態轉移方程:當 n == 1 || k == 1 時,f(n, k) == 1, n為1,那麼只能為1; 而k為1,那麼