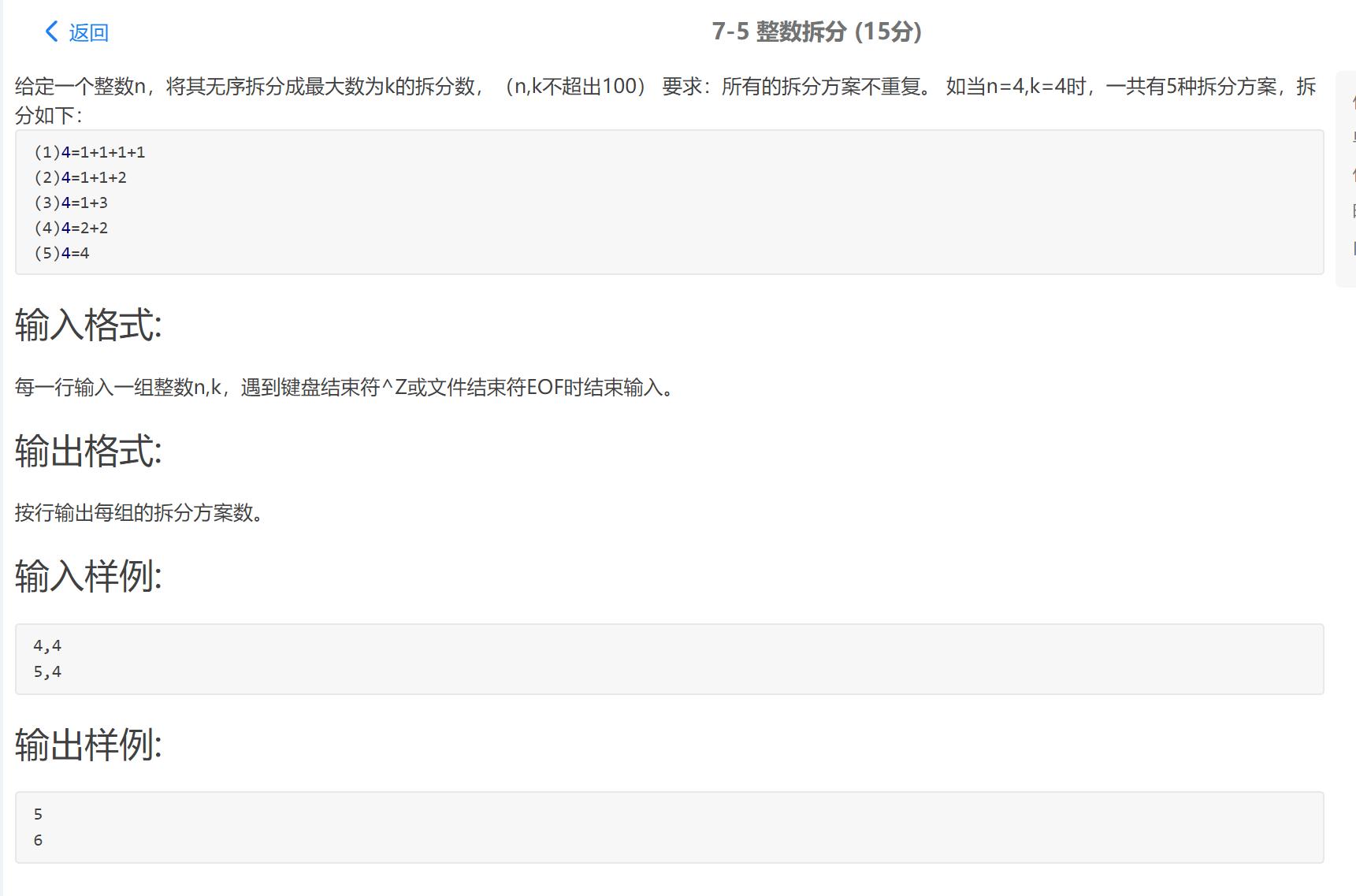
##題目描述  ###考試時思路 本菜狗考試的時候，第一扁打了純dfs，15分拿了9分 後面看了時限400ms，多組資料，以為會卡常數，然後就想著先dp打表然後再直接O(1)查詢 後面發現自己想多了，資料有點水……dfs+dp都可以過 然後打表，找規律找到了後半段$[\cfrac{i}{2}+1,i]的規律 `for(int j=(i>>1)+1;j<=i;j++)dp[i][j]=dp[i][j-1]+dp[i-j][i-j];` 沒有聯想到第一段的規律，歸根到底還是自己dp太弱了 ###正解思路 dp[i][j]表示，n=i,j=k時候，總的劃分方案數 當j>i時候，就例如數只有4，上限卻是5，所以dp[i][j]可以用dp[i][i]表示 i劃分為最大為j的若干個數，分兩種情況 一種情況就是裡面有j,1*dp[i-j][j] 另一種就是裡面沒有j,dp[i][j-1] 所以最後的狀態轉移方程為`dp[i][j]=dp[i][j-1]+dp[i-j][j]` ###程式碼實現 ```